Anne Chapman
School of Education
Murdoch University
This paper outlines basic assumptions and principles of the theory and practice of social semiotics in order to develop a framework for understanding language practices in the mathematics classroom. In this framework, school mathematics is a social practice in which teachers and learners use language as a resource with which to construct mathematical meanings. It is argued that mathematical meanings are constructed in part through specific language practices and formations; moreover, that learning mathematics is very much a matter of learning to speak 'properly' in the classroom. Reference to a recent study of the relationship between language and learning in school mathematics illustrates implications of social semiotics for educational research.
This paper is a response to the recent trend in approaches to the study of language and mathematics towards a concern with the social, interactive nature of meaning and learning in the classroom. The different approaches typically share a concern with four key factors in mathematics learning: cognitive, linguistic, social and contextual. Yet, too often, these factors are treated as disparate and unrelated. I want to outline here ideas from the theory of social semiotics in order to provide a perspective on language and mathematics learning that deals with the complex interrelation among these factors. This perspective positions school mathematics as a social practice in which language is a resource for meaning. Essentially, I want to establish some of the main principles of social semiotics and show how they relate to the language practices of mathematics education. I will refer to the findings and implications for educational research of my own recent study of the language practices of school mathematics that works with this social semiotic perspective.
Social semiotics
Social semiotics, a synthesis of contemporary approaches to the social production of meaning, is based on formal, or mainstream semiotics, a theoretical approach to the study of signs and sign systems. Semiotics can also be considered more generally as the study of meaning, its central concern being how meanings are generated. Social semiotics takes this concern in a particular direction. As the term suggests, it focuses on social interaction: on how people construct systems of meaning, rather than on the systems themselves. Social semiotics views 'meaning' as an active process, generated through social interaction.
The central notion of social semiotics is that all meanings are made. They do not exist as objects or concrete facts. Rather, they are constructed through systems of signs. A sign is some physical thing that stands for, or refers to, something else. A painting or photograph is an iconic sign. Colours and gestures can also be signs. A word, either spoken or written, is a linguistic sign. It has a physical form, either the spoken sound or the written letters, and is associated with certain mental concepts. The physical form of the sign is termed the signifier, and the concept of what it refers to, the signified (de Saussure, 1974). Signification, or meaning making, is "the relationship of a sign or sign system to its referential reality" (O'Sullivan et al, 1983: 215). What is of concern in social semiotics is the nature of the relation of signified to signifier, that is, the signifying practices, which are the processes of meaning making. This relation is not purely linguistic. Rather, it is a social relation (Walkerdine, 1982). Meaning relations cannot be understood outside of their use in the social practices of some community (Lemke, 1987: 218).
Marks and Mousley (1990) point out that mathematics is now widely accepted as a semiotic system. Clearly, mathematics is a system of signs. In fact, mathematics comprises many systems of signs with which people make sense of the world. The symbol 5 provides a simple example. It is a mathematical sign. It stands for some thing. But the sign 5 itself does not have meaning. People construct meanings for it following the conventions of mathematics. Its meaning may be derived by counting or ordering, or it may be the result of an arithmetic operation, or of measuring a distance. Different meanings might be made about the number 5 by different people, or by the same person in different contexts. The important point is that there are shared meanings for each different context. These shared meanings are constructed and developed using social conventions, such as ordering, counting and measuring, which are recognized as ways of making meanings.
The shared meanings of mathematics include mathematical techniques, that is, procedural knowledge, as well as conceptual knowledge. Knowing how to perform actions in certain ways is a strong feature of school mathematics. Standard written algorithms often provide a focus for mathematics lessons. Knowing how to 'do' long division, for example, really means knowing how to do it in the 'correct' way. Factorising binomial expressions involves performing a pattern of actions that is likely to be practised and repeated many times in the mathematics classroom. The method is as important as the result. Actions such as these are ways of making meaning in mathematics. They are semiotic practices that make sense in mathematics. They are also an important part of what presently constitutes school mathematics.
Language and mathematics: Semiotic resource systems
An important aspect of social semiotics for understanding the role of language in school mathematics is that it allows an understanding of both language and mathematics as resource systems: systems of possible ways of meaning'. Semiotic resource systems comprise what can or might be said or done. What is actually said or done is a semiotic formation. Lemke's (1990) description of social action in terms of semiotic resources and semiotic formations generalises from Halliday's (1978) model of language as 'meaning potential':
Language is being regarded as the encoding of a 'behaviour potential' into a 'meaning potential'; that is, as a means of expressing what the human organism 'can do', in interaction with other human organisms, by turning it into what he (sic) 'can mean'. What he can mean (the semantic system) is, in turn, encoded into what he 'can say' (the lexicogrammatical system, or grammar and vocabulary). (Halliday, 1978: 21)
Language and mathematics can both be understood as semiotic systems: systems of meanings and systems for the construction of meanings. They are also both resource systems for the creation of meanings. It is perhaps easier to view language than mathematics in this way. People constantly use language to make sense of their experiences. In schools language is used as a tool with which to construct the 'content' of the different subject-areas. Mathematics is also a resource system. It is a resource for making the meanings of other school subject areas, such as science and social studies. Language is used to construct and share mathematical meanings; at the same time, there is a system of potential mathematical meanings. There are things that it is possible and appropriate to say and do that make sense in mathematics classrooms. School mathematics comprises these possible ways of meaning. The thematic formations of semiotic resource systems are most often realised in language. They may also be expressed in non-verbal mathematical representations, such as symbolic, tabular or diagrammatic forms, but in the classroom verbal language is the fundamental process for the shared construction of mathematical meanings.
Register
Particular kinds of activities require particular kinds of language. Very often, the nature of an activity can be determined by the style of language use. In this sense language reflects the activity. At the same time, language can help to create a situation. A change in the style, tone or vocabulary of language can signal a new type of activity.
The linguistic term register refers to the particular kind of language used in a specific situational context. Halliday uses the term to describe 'a set of meanings that is appropriate to a particular function of language, together with the words and structures which express these meanings' (1978:195). The mathematics register is made up of specific uses of language for mathematical purposes. This includes the words and structures of mathematics, both spoken and written, and the meanings they express. In the mathematics classroom there is an implicit requirement to use language in certain kinds of ways. Teachers introduce and model 'mathematical' words and language structures which are privileged over other language forms. Learning mathematics involves learning its register.
Register is characterised in three ways: field, tenor and mode (Halliday, 1978). Field refers to the social activity that is happening, in which language plays a part. It describes what people are doing, and includes topic and subject matter. Tenor refers to the roles and personal relationships of participants in the social activity. Thus it includes power, status, feelings and attitude. Mode refers to the means of communication, the way in which the interaction happens and the way it is organized. This might be speaking or writing, or using a symbolic form of representation. Acquiring a register requires facility with each of these three aspects. This means that it demands more than learning the appropriate words and structures. It also involves being able to predict the kind of language appropriate to field, tenor and mode for a particular context of situation (Green, 1988).
Lemke approaches the notion of context of situation from a particular perspective. He states that every context of situation has two aspects: an interactional aspect and a thematic aspect:
. . every act is assigned a meaning both in the interactional context and in the thematic context and contributes to both interaction and thematic development, having the power to radically alter as well as to maintain both the interactional and the thematic situations. (1982a:12)
Register, then, can be characterised in two ways: by its thematic context, which equates with field, and by its interactional context, which equates with the combined categories of tenor and mode. Lemke asserts that "what characterizes a particular register is the way its 'meaning potential' is restricted within the 'meaning potential' of the full language" (1982a: 32). If familiarity with a particular context of situation allows us to predict features of its register, then we can say that the register has a 'meaning potential'. There are possible uses of language and possible meanings for every situation. These possibilities are enabled and constrained by the situational context.
Describing the register of the science classroom, Lemke states:
The effective language of the classroom is the shared language of pupils and teachers, a constantly changing hybrid of common parlance, our ordinary ways of talking, with the registers which teachers and pupils may use in other settings (in textbook reading, in university lectures, talking with peers, etc). (1982b: 263)
Green (1988) also points out the need to see school subject registers as what he calls a family of registers. The register of the mathematics classroom includes a number of different registers which come into play in different situational contexts. Clearly, there is the register of 'formal' or 'technical' mathematics. There is also the register of teaching - the different kinds of language used by the teacher in the different social activities of lessons. For example, the language used by the teacher in a whole-class discussion might differ from that used in a teacher-student dialogue, or from a monologue introducing a new concept. These various kinds of language within the school mathematics register will be more mathematical or less mathematical, depending on the nature of the activity.
The school mathematics register
In this section I describe features of the register of school mathematics and, in particular, some ways in which language comes to be more mathematical. The school mathematics register is most readily identifiable in terms of field. It has a highly specialised vocabulary: both words appropriated and redefined from everyday language, such as mean, obtuse and improper, and words specific to subject-area mathematics, such as hypotenuse and integer. The reinterpretation of existing words is a trait of school mathematics and of mathematics generally. The word show, for example, in the context of the mathematics lesson becomes an instruction to prove or justify, rather than its everyday or non-mathematical meaning, to display or point out. The word set, which has a number of nonmathematical meanings, takes on specific properties in mathematics. There are numerous examples of the mathematical use of everyday English words, including the following:
| result | prove | establish | simplify | negative | solution |
| identity | image | relation | universal | chord | face |
| index | multiple | network | intersection | mean | mode |
| operation | origin | multiple | plane | prime | range |
| variable | rational | product | real | reciprocal | closed |
Words become specific to mathematics in a number of ways. As Halliday (1978) points out, mathematical English includes many words borrowed from other languages.Examples include: (1) from Latin: subtract, series, acute, binary, identical, frequency, prism, apex, coefficient, node, continuous, median, formula and matrix; (2) from French: domain, evaluate, cone, gradient, multiple, correspondence, similar, cube, dividend, symmetry and cylinder; and (3) from Greek: isosceles, isometric, logarithm, and pi.
The school mathematics register tends also to create new words out of words or parts of words from other languages. The word histogram, for example, is made up of the word elements gramme (from French) and historia (from Latin), and hypotenuse from the Greek words hypo and teinein.
Phrases or groupings of words can also become recognised as technical terms. The school mathematics register has an abundance of these locutions, such as:
| degree of freedom | identity mapping | cumulative frequency |
| frequency diagram | direct route | prime factor |
| multiplicative inverse | right angle | ordered pairs |
| highest common factor | rounding off | empty set |
| squareroot | identity element | directed numbers |
The examples provided above are illustrative of words and phrases belonging to the register of school mathematics. They can also be classified into the subregisters of mathematics. School mathematics includes a number of topics or areas of study, such as arithmetic, algebra and geometry, each of which is taught as a distinct subject-topic and has its own register.
The language of school mathematics involves spoken and written forms. As the spoken language of the classroom becomes more mathematical, it often becomes closer to the written forms typically found in mathematics textbooks. Written mathematical language includes specialised systems of symbols, which are often combined with verbal language to create expressions such as the following:
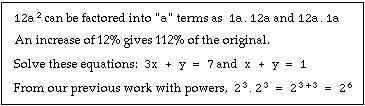
Read aloud, these expressions would not be out of place as part of the spoken language of the mathematics classroom. Students learn that speaking mathematically very often means speaking the language patterns characteristic of the written mathematics textbooks. It is necessary then to take into account this close connection between written and spoken mathematical language.
While certain features of the mathematics register, such as those described above, can be isolated and identified, the language used in the mathematics classroom cannot be regarded as a fixed or distinct set of words. Words alone do not carry the meanings of school mathematics. To operate and control the register of school mathematics, learners need to master its complex systems of meaning relations, its 'ways of thinking' within the context of everyday usage.
Meaning and context
The term 'semiotic formations' (after Foucault's (1970) 'discursive formations') describes the "repeated, institutionalized ways of talking and doing in a community" (Lemke, 1987: 218). A semiotic formation is a pattern of meaningful action that uses semiotic resources, such as language. All school subject-areas draw on language as a resource, yet each has its own ways of speaking and behaving. The following very brief transcripts exemplify ways in which teachers and students use language appropriate to the context of situation:
| Example One | |
| Teacher: | See how you go with these other stories. See what you can say about what they have in common and what makes them different. |
| Example Two | |
| Teacher: | OK. Work through it step by step. Remember to label both axes. |
| Daniel: | Should we put in all the points? |
| Teacher: | Of course, but labelling is what I'm looking for. |
| Example Three | |
| Teacher: | All right people, complete the chart by finding out the controls for these other examples. Then do the map. |
| Student: | But Sir, how do we know what the controls are? |
The kind of language used in each of the above examples reflects something of the situation in which it was produced. It is not difficult to recognise that they belong to the different school subjects of English, mathematics and geography, respectively. None of these examples includes much 'content matter', yet each belongs to an identifiable register. The point I am making here is that in order to understand the language practices of the classroom, it is important to examine the way in which something is said, as well as what is being said.
I want to take up here Lemke's notion that every act, including talk, has both an interactional and a thematic meaning. That is, it contributes to two interdependent discourse structures: activity structures and thematic structures. Activity structures are the routines that make up classroom life. They are "recurring functional sequences of actions" (Lemke, 1987: 219). These actions can be verbal or non-verbal. Classroom dialogue typically includes activity structures such as 'homework review', 'teacher-led discussions', and 'teacher question/student-answer'. The different lessons of a subject-area tend to share the same sorts of activity structures. In school mathematics, 'oral arithmetic sessions', and 'worked blackboard examples' are common activity structures. These are routines that typically occur in a mathematics lesson. Different mathematics lessons on different topics might have their own activity structures, such as drawing graphs in algebra, working with calculators in arithmetic and constructing angles in geometry.
Thematic structures, also sometimes referred to as thematic formations, are the "recurring patterns of semantic relations among the themes and concepts of a particular way of speaking about a subject" (Lemke, 1987: 219). These are the familiar ways of speaking about a particular topic or theme. Texts that construct the same patterns of meaning relations have the same thematic structure. A thematic structure can be a unit topic, or the theme of a single lesson or of a small-group discussion. For example, within a lesson on linear functions, a textbook definition of the term linear, a whole class discussion and an example of a linear graph drawn on the blackboard might all share the same thematic system.
Activity structures and thematic structures are examples of semiotic formations. The assumption underpinning the view that everything that is said or done contributes to both of these structures is that meaning cannot be separated from action. An important implication of this view is that in order to understand the use of language in the classroom it is necessary to consider its role in both the enactment of activities and in the development of the content matter of the lesson.
The activity structures and thematic systems within the mathematics register combine to produce the particular discourse that I have been calling school mathematics. Consider, as an example of the interrelation between activity structures and thematic structures in language, the following interaction between the teacher and two students, Arthur and Stuart, in the lesson referred to above on linear functions:
| Teacher: | So far we've had functions we could call linear. What were the distinguishing features of our linear functions? Arthur? |
| Arthur: | A straight line. |
| Teacher: | They formed a straight line. What else can you tell me about linear functions in terms of the tables of values? Stuart? |
| Stuart: | It always went up by the same. |
| Teacher: | It always went up by the same. So how did you think that, how did you know that it always went up by the same amount? |
In this discussion, the language of all three participants contributes to the development of a system of thematic relations between 'linear functions', 'straight lines' and 'tables of values'. These are the thematic items of the discussion. The relations being constructed in this brief episode are part of a broader discussion which includes other thematic items, such as 'rules' and 'difference patterns'. All of these items and the relations among them are part of a highly standardised thematic formation for the topic of linear functions. Both student responses are quite brief It is the teacher who comments on and elaborates these responses. He is signalling an appropriate way of talking about linear functions. The essence of Arthur's answer is correct, but the teacher puts it into a more 'proper' sentence structure. Stuart's term "the same" is restated by the teacher as "the same amount". The speakers are apparently making sense with each other as they develop a more mathematical way of talking.
The language of this episode also contributes to the development of a particular activity structure. The episode can be understood as two separate dialogues: between the teacher and Arthur, and between the teacher and Stuart. These dialogues exemplify a pattern of activity typical of this classroom: the teacher asks a question of an individual student, the student answers; the teacher evaluates the answer and then goes on to question another student. In this case, neither Arthur nor Stuart has volunteered to answer the teacher's question. Nevertheless, having been chosen by the teacher to do so, each provides an answer, contributing to this regular activity structure. The teacher, too, maintains the typical pattern. He confirms each student's response by restating it in a slightly different way. This is a common strategy for this teacher. Arthur's answer, "a straight line", is restated as "they formed a straight line", thus made over into what is evidently for the teacher an acceptable response. Stuart's answer, "it always went up by the same" is also acceptable. The teacher confirms this by repeating it; but in changing the term same to "same amount" he is quite subtly signalling a more appropriate, or more mathematical, way of speaking.
The brief analysis of the above example shows the interrelation between activity structures and thematic structures. It is clear that language contributes to both structures at the same time:
These two aspects - the dynamics of social interaction and the development of the thematic content of the subject being taught - are in principle separable, but in practice they are never really independent of one another, because they are simply two aspects of the same flow of behaviour. We separate these aspects in the analysis only so that we can then look at their relations to one another. (Lemke, 1985: 13)
This perspective that language contributes to both activity structures and thematic structures has several implications for understanding language practices in school classrooms. The first implication is that meaning cannot be separated from social action. In order to understand how the themes of a subject-area are developed, it is also necessary to consider the interactional contexts in which their meanings are constructed. That is, meaning is always produced in context; it cannot be separated from social action. A second implication is that the ways of speaking that are appropriate to a subject-area are developed as part of the social practices of classroom interaction. Students do not come to the mathematics classroom armed with a knowledge of how to speak mathematically. They learn this language as they learn mathematics.
Language practices in school mathematics
The social semiotic perspective provided in this paper frames my recent study of the spoken language practices of school mathematics (Chapman, 1992). This study is essentially an investigation of the relationship between language and reaming in the mathematics classroom. It argues that mathematical meanings are constructed in part through specific language practices and formations, based on an empirical investigation of the spoken language of the teacher and learners in a Year Nine mathematics class over a ten week school term. Close analyses of transcripts provide a descriptive and interpretive account of the language practices considered characteristic of school mathematics.
Episodes of classroom talk were analysed, often several times, and using a range of methods of semiotic analysis, for general themes and patterns. Some of the language of the transcripts could be readily classified as mathematical or non-mathematical. However, most of it was some mix of what I have been calling here 'more mathematical' or 'less mathematical' language. What became clear from close readings was that there were continual and frequent shifts between more and less mathematical language. Moreover, these shifts occurred within very short interactions. The overall shift, though, from episode to episode, and within whole lessons, seemed to be towards a more mathematical kind of language. What became evident was that the shift towards more mathematical language is an integral part of the language practices of school mathematics. My argument is that it is within this shift that mathematical meanings are constructed: learning mathematics in school classrooms requires this shift.
I have outlined here only one of the outcomes of the study in order to point to particular implications of social semiotic theory for educational practice in mathematics and subject-area learning more generally. Primarily, attention must be paid to the role of language in classroom learning. Language practices are not just important, but essential, to mathematics learning. The language demands of mathematics must therefore be made more explicit to afford reamers greater control over their meaning constructions. Further, critical learning in any subject area involves making use of multiple semiotic systems, one of which is language. It is the deployment of these systems that constitutes the 'social construction' of meanings .
The study referred to demonstrates that learning mathematics is very much a matter of learning to speak 'properly'. There is a pervasive and continual requirement, which is often implicit, to shift towards increasingly mathematical language. If this finding is generalisable to other subject-areas, then such research studies will challenge existing assumptions of language and learning on which they lie. Both the processes and outcomes of classroom learning may well require a radical reappraisal. The perspective I provide in this paper views classroom learning as a social practice, in which teachers and learners use language in social interaction to construct meanings. Through these understandings of the social construction of meaning through language, social semiotic theory clearly has much to offer educational research.
References
Chapman, A. (1992). Language practices in school mathematics: A social semiotic perspective. Unpublished PhD dissertation, Murdoch University.
de Saussure, F. (1974). Course in general linguistics. London: Fontana.
Foucault, M. (1970). The archaeology of knowledge. New York: Pantheon.
Green, B. (1988). Subject-specific literacy and school learning. Australian Journal of Education, 32(2), 156-79.
Halliday, M.A.K. (1978). Language as social semiotic. London: Edward Arnold.
Lemke, J.L. (1982a). Classroom communication of science. (Final report to the US National Science Foundation.) Arlington, VA: ERIC Documents Reproduction Service No. ED 222 346.
Lemke, J.L. (1982b). Talking physics. Physics education (UK), 17, 263- 267.
Lemke, J.L. (1985). Using language in the classroom. Geelong, Vic: Deakin University Press.
Lemke, J.L. (1987). Social semiotics and science education. The American Journal of Semiotics, 5(2), 217-232.
Lemke, J.L. (1990). Talking science. Language, learning and values. Norwood, NJ: Ablex Publishing Corporation.
Marks, G. & Mousley, J. (1990). Mathematics education and genre: Dare we make the process writing mistake again? Language and education. 4(2), 117136.
O'Sullivan, T., Hartley, J., Saunders, D. & Fiske, J. (1983). Key concepts in communication. London: Methuen.
Walkerdine, V. (1982). From context to text: a psychosemiotic approach to abstract thought. In M. Beveridge (Ed.). Children thinking through language. London: Edward Arnold.
| Author: Anne Chapman teaches in the School of Education at Murdoch
University. She has researched and published in the areas of language and
learning in school mathematics, and literacy and numeracy in adult education.
Her current research work concerns the pedagogical relationship between literacy and numeracy.
Please cite as: Chapman, A. (1993). Language and learning in school mathematics: A social semiotic perspective. Issues In Educational Research, 3(1), 35-46. http://www.iier.org.au/iier3/chapman.html |
© 1993 Issues in Educational Research
Last revision: 5 Dec 2013. This URL: http://www.iier.org.au/iier3/chapman.html
Previous URL: http://education.curtin.edu.au/iier/iier3/chapman.html
Previous URL from 2 July 1997 to 7 Aug 2001: http://cleo.murdoch.edu.edu.au/gen/iier/iier3/93p35.htm
HTML: Clare McBeath [c.mcbeath@bigpond.com] and Roger Atkinson [rjatkinson@bigpond.com]