IIER logo 4
Issues in Educational Research, 2016, Vol 26(4), 576-591
[ Contents Vol 26 ] [ IIER Home ]

Basic numeracy abilities of Xhosa Reception year students in South Africa: Language policy issues

Nosisi Nellie Feza
University of South Africa

Language in mathematics learning and teaching has a significant role in influencing performance. Literature on language in mathematics learning has evolved from language as a barrier to language as a cultural tool, and recently more research has argued for use of home language as an instructional tool in mathematics classrooms. However, the complexity of language is becoming another emerging challenge from bilingualism to multilingualism in different contexts. The need for access to mathematics knowledge has prompted debate about language policies that are inclusive of previously under-represented languages, especially in South Africa. This paper therefore extends this debate by exploring Reception class students' basic numeracy abilities and their numeracy levels to see if they speak in accord with the current language policy of South Africa and to assess whether the curriculum connects with the students. A concurrent mixed methods design was employed to investigate context and numeracy knowledge levels for a sample of 26 Reception class students from low socio-economic backgrounds. Both descriptive and thematic analyses were conducted to analyse the biographical, contextual and interview data collected. The findings reveal that the literacies experienced by students in their early ages of life are different from those perceived by policy makers, researchers and curriculum designers. This paper calls for more studies that are interdisciplinary as new identities and literacies are developing.

Introduction

Language policy-making in South Africa is complex and needs insight from research. Setati's (2005, 2008) work indicated very clearly the role that mother tongue instruction/tuition plays in making sense of mathematical ideas. Her work gave insights into classroom practices in contrast to expectations on language issues in mathematics education. She indicated that although it is not part of language policy, code-switching occurs without planning as teachers argue that it happens as the need arises. This code-switching (when a speaker alternates between two or more language) has its pros and cons; it allows students to understand teacher explanation while on the other hand it denies students the opportunity to acquire proficiency in one language. Students develop conceptual understanding by sharing their mathematics thinking and understanding, while using home language. In this case home language becomes a tool for sense-making of mathematical ideas, as revealed by Setati (2008) and Feza-Piyose (2012). In these studies home language is demonstrated by students as a useful tool to communicate thinking and explain their mathematical process in solving problems. The literature has argued for mother tongue instruction for some time now. Khitsy and Morales (2004) highlighted the inequities in learning that are experienced by non-English speaking students. It is important to note that students do come with diverse, rich languages that influence their frame of reasoning and therefore denying them use of these languages is a marginalising factor (Bishop, 1985). Vygotsky (1978) highlighted the importance of personalisation of meaning which in his words was described as "internalisation". This internalisation of ideas happens only if the language spoken is understood and used fluently to communicate ideas. The TIMSS 2011 findings (Mullis, Martin, Foy & Drucker, 2012) support this notion as they indicate clearly that students' performance is positively associated with the language of the test when it is the language spoken at home.

South African education policy asserts that Grade R (reception class) students should learn in their home languages (DoBE, 2014). Grade R is the first year of school in South Africa for 5 to 6 year old students and it is a bridging year between pre-school and formal schooling. Research supports this practice as Heugh (2012) indicated that more time spent by learners learning in their mother tongue has positive benefits for their performance. In view of such recommendations, this policy stipulation of mother tongue instruction for foundation phase (Grade R to 3) learning came to being in South Africa (DoBE, 2014). Mullis et al (2012) in The PIRLS 2011 International Results in Reading report revealed that students who take the international language test in their home languages perform better than those taking tests in a second or third language. These international findings demonstrate clearly that this language challenge does not belong solely to the South African context but to other countries. Nunan (2003) discovered that English as a universal language in the Asia-Pacific region created irregularities and inequities to effective language teaching as teachers were not proficient with English.

Internationally, there is a need to understand the complexity of language in mathematics learning and teaching. The demographics of the global community have changed due to increasing migration and immigration. Kiefer et al (2009) revealed that poor performance in mathematics is influenced by proficiency in academic English, hence they argued for development of academic language skills that are central to performing sophisticated mathematical tasks. This recommendation opens debate as they have not unpacked how this academic language can be developed amongst students. Research has to inform this community on how to address these challenges. Already code-switching is employed in different parts of the world (Salehmohamed et al., 2014; Selamat, 2014). What is not clear to date is the impact of such practice. Despite much support of the use of home language for learning mathematics, little is known about pre-school students' language skills in counting as they enter school.

The aim of this paper is to share linguistic numeracy levels demonstrated by Reception class students (Grade R) prior their formal engagement with learning in the Reception class. In this case, counting skills possessed by learners from their early experiences will be explored to see if the findings promote mother tongue learning. The paper also aims to explore the numeracy language abilities these students enter schools with. Therefore this paper aims to respond to the following research questions:

  1. How advanced are Reception class students in terms of learning trajectories (Clements & Sarama, 2009) in using their home language for counting before entering formal schooling?
  2. Does the developmental progression observed in home language mediate counting concepts further?

Language and mathematics learning and teaching

Research on language and its impact on the learning of mathematics is very broad. Some researchers argue that language can constitute a barrier when the language of the dominating group becomes the main language of instruction (Winsor, 2007; Barwell, 2002. However, this research is challenged by others who emphasise the need to recognise the impact of ignoring other people's languages as learning tools (Adler, 1998, 2001; Setati & Adler, 2001). These authors contribute to the literature that argues for pluralism. In response to this, further research then leads to more arguments that a home language is cultural capital possessed by all individuals and therefore should be used as the capital it is (Heugh, 2012). As a result, policies have changed and nowadays assert that home language should be used to address exclusion and inequities and also to promote access to knowledge. On the other hand, there is research that proposes the nurturing of language proficiency and language efficiency (Essien & Setati, 2007).

English language proficiency for mathematics learning and teaching for second language students

Essien and Setati (2007) asserted that improving English language proficiency of non-native English-speaking students improves their mathematics performance, when English is their language of instruction and assessment. Their study conducted an intervention that improved English language proficiency of Grade 9 African students, with results indicating a higher performance of the experimental group after intervention. The findings of this study support the literature that promotes learning of mathematics through a well-understood language. This association between English language proficiency and mathematics achievement has also been highlighted in United States studies on students whose home language is not English (Beal Adams & Cohen, 2010; Brown, Cady & Lubinski, 2011; Henry, Nistor & Baltes, 2014; Kieffer, Lesaux, Rivera & Francis, 2009). However for the early years of schooling there seem to be only a limited number of studies focusing on language issues in mathematics teaching and learning. This has implications for understanding the continuing poor performance in mathematics by South African students.

South African language policy

The group of students investigated in this research all speak isiXhosa, one of the 11 official languages, as their home language. According to the Language in Education Policy (DoE 1997) and the Revised National Curriculum Statement (DoE 2002), Grade R students researched in this study should learn in their mother tongue. This policy is supported by researchers such as Alexander (1999), Ball (2010), Cummins (1996), Heugh (2002) and Skutnabb-Kangas (2000), who promoted the use of mother tongue tuition and who asserted that mother tongue use lays a rich foundation for obtaining reading skills that can later be transmitted to other languages. Bialystock (2006) and Klass and Trudell (2011) argued that a discrepancy between the language of teaching and the home language spoken by learners hinders learner involvement, inhibits content learning, and makes critical thinking difficult. Hence much advocacy for mother tongue instructions, for example as Mbatha (2014) who claimed that mother tongue is a starting point. Therefore, this paper sets out to investigate the numeracy mother tongue capabilities and potential of Grade R students, and how these capabilities are aligned with the language of instruction.

Number learning trajectories

Counting concepts for young children need to be understood for a firm foundation of number knowledge and useful development. Feza (2015) gave a detailed account of the developmental progression levels, as hypothesised by Clements and Sarama (2009). She argued that innate abilities of young students form a rich foundation for developing these concepts. In summary, Feza (2015) listed the concepts in a linear way as verbal counting/ rote counting; object counting/ one-to-one correspondence; cardinality/ response to the how many question; counting backwards; skip counting; and counting on. She also mentioned the skill of subitising (promptly seeing how many), which Clements and Sarama described as an innate skill that could be further developed for number patterns and multiplicative knowledge of numbers (Clements & Sarama, 2014). These basic concepts play a significant role in using young students' activities in composing and decomposing, that later develops the knowledge of basic operations. This paper investigates whether these reception class candidates have any of this knowledge, and to what level of understanding.

Zone of proximal development (ZPD)

In investigating the levels of understanding of number of these Reception class students, Vygotsky's (1978) theory of ZPD is regarded as the best theory to employ in an analysis investigating how these understandings could be aligned with learning of the curriculum. ZPD can be summarised as the actual developmental level of the student and the potential the student demonstrates for developing; meaning readiness for reaching the next level. This theory will then assist in aligning students' levels of understanding number to the curriculum expectations. It will also assist in determining the level of expectations the South African curriculum assessment policy statements have for the students; whether they are aimed too low or too high. This paper will also attempt to give a critical view of the Reception class curriculum in number development, with reference to ZPD that will be measured by learning trajectories (Clements & Sarama, 2009). The strength of this theory in the context of this study lies on the mediation and integration of culture as a tool for learning and developing a student (Feza, 2013). Language of the student becomes the internal tool the students bring to school to assist them to make sense of the new ideas confronting them. Thus, the aim of this paper is to explore whether the current language policy of South Africa speaks to students in current Grade R classrooms, and whether curriculum expectations in number development, specifically counting concepts, are at an achievable level for this group of students.

Methodology

An extensive literature has been documented Spaull and Kotze (2014) and Brown, Cady and Lubinski (2011), concerning the disadvantages of low socio-economic background with respect to stimulating the minds of young students. This paper seeks to reveal the consequences of these disadvantages, if any, for students in Quintile 1 schools (no-fee schools) of South Africa, and to make observations about language policy alignment with these students' home language. This requires both a quantitative analysis of the background of these learners and an in-depth, qualitative analysis of their counting knowledge. Therefore, this research adopted a mixed-methods approach. The research questions for this paper required a concurrent procedure which Creswell (2003) described as the use of quantitative and qualitative analyses to give a comprehensive analysis of the problem investigated. Therefore this paper uses a concurrent procedure to give an account of students' background, and what these circumstances have exposed them to before their formal schooling commenced. This will position this paper to support or challenge the extant literature about the role played in mathematical stimulation by the students' circumstances, in the regional context of the Eastern Cape of South Africa.

Participants

The district where this study was conducted has a number of municipalities. One of these municipalities has six primary schools that participated in a National Research Foundation funded study. The participants in this research come from five of the six primary schools. The primary school excluded was missed due to time constraints and teacher excursion activity in the morning, as the researchers revisited and arrived after the reception classes were dismissed, being tired from their excursion. Twenty-six Reception class students were selected randomly from class lists by first asking teachers to separate the boy's list from the girl's list. Names written on pieces of papers were put in two bowls and a student was asked to pick one from each bowl. The teacher had to make sure that all students with names in the bowls were present at school on the data collection day for each Reception class; only two students were selected to participate in the interviews. As conducting interviews with young students is time consuming, the interview sample had to be limited to two students per class. This was considered as adequate, given that the aim of this research was to gain initial insights into the students' ZPD. Two students per class allowed for developmentally appropriate engagement, as students could engage with manipulatives with no pressure of time. This study was conducted at the beginning of the school year before formal instruction commenced, thus the data presented here concerns students' knowledge before they started learning in a Reception class.

Instruments

A mixture of unstructured and structured questions were used to develop the interviews. The main purpose of this was to allow students to first play with the manipulatives with no expectations and also feel free to engage with the researcher. These interviews were developed and tested by the author with ten five-year-old children from her church in the Gauteng provinc. A group of 36 young children between 4 to 9 year old meet in this church every Saturday to engage in activities. The researcher asked the permission of parents to conduct the interview with their five year old children numbering about 17; 16 showed interest. All parents consented, but about six of the 16 five year old children played when interviews were informal and ran outside when numeracy questions began. These interviews were conducted individually over three Saturdays. The analysis of this pilot assisted the researcher in improving the provision of materials to learners, as having all of them in sight leads to disruption. The manipulatives for counting had to be alone on the table with no other manipulatives in sight when the interview started, and students needed about 5 minutes time to play with them, mostly sorting them by colour, otherwise they were not willing to stop while they were sorting or making structures. Their responses to the questions gave insights into their counting skills, knowledge and language. The aim of these interviews was to elicit the number knowledge and geometric knowledge that students possess before entering formal schooling. However, this paper discusses only number knowledge with a specific focus on counting.

Data collection

Two groups of five researchers visited three schools per group to conduct the interviews with the Reception class students. Both groups video recorded the interviews and also took field notes. Each interview lasted about 15 minutes with each student. Manipulatives/physical materials such as counters (Unifix Cubes and bottle tops) were provided during interviews to give students opportunities to use them and allow the researchers to observe students' actions and interests.

Data analysis

The questions posed by this research require the use of both quantitative and qualitative investigation for a comprehensive, in-depth exploration of counting developmental levels acquired in home language by Grade R learners, and the understanding of their context. A descriptive analysis of students' home backgrounds was deemed important for obtaining a comprehensive picture of the student investigated. Therefore, a descriptive analysis of students' background data will be conducted. This paper aims to reveal both the actual counting knowledge levels of students together with their potential including their language capabilities.

The biographical and context-based data was separated and entered into an Excel spreadsheet for quantitative analysis, aiming to obtain frequencies and groupings of data. Qualitative data from the video recordings of interviews was transcribed into a Word document, giving each line a number for analysis, while the field notes were entered separately, using the same format of numbering. The aim in separating the two sets of data was to analyse separately and then triangulate together at the coding level of the analysis. The typed data was then shared amongst two researchers for conducting individual analyses, as the two researchers agreed to write separate papers each with a different focus upon the data.

Each line was annotated with low inferences throughout both data sets. These low inferences were then grouped together in a table for each data set to make it easy to work with them. They were then colour coded according to similarities with the aim of finding patterns. Those low inferences that were not matching others were also highlighted using different colours and those that were contrasting some were also colour coded differently. Analytical memos were written summarising the observations and incorporating raw data to support the emerging patterns. The codes then started emerging when raw data was revisited and each researcher brought forward their separate codes. The two sets of codes from the two researchers were then triangulated through discussion, revisiting the raw data for empirical evidence and confirmation. Both researchers shared their analytical memos in strengthening the codes. Consensus codes were developed and were triangulated with the theory of learning trajectories for counting (Clements & Sarama, 2009, 2014). Analytical themes emerged from this analysis, and a thematic report will be presented in the next section.

Findings

This paper will first present the students' background quantitatively with the aim of situating this paper with the research that relates to students from low socio-economic backgrounds. As a researcher, I do not see these students as poor as their cicumstances are similar to mine as a child. Hence, I use my perspective of describing myself as a child who never knew myself as being poor. Although this paper is not focusing on labelling, I challenge the concept, following the linguistic literature on the cognitive effects of such labelling. The literature asserts that the words we use to define what we see, control what we see (Carrol, 1997). This means if I portray a child as poor, then the child may not strive to get out of the poverty but will remain in poorness. Therefore, the low socio-economic status in this paper does not refer to the student, but describes the school and the home.

The context

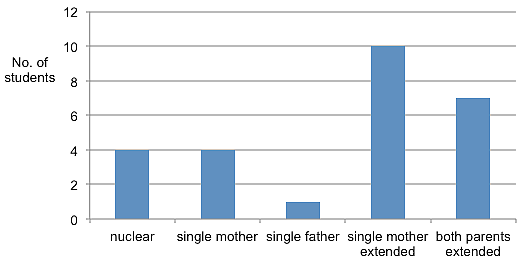
At the time of the study, all students in this research attended no-fee-paying schools of South Africa, known as Quintile 1 schools, fully funded by the government. Figure 1 below presents the family structures these students come from.

Figure 1

Figure 1: Family structures of students

Figure 1 illustrates that the most common home structure for these students is extended families of single mothers. Extended families in the South African context are more prevalent amongst the black community due to the distribution of wealth that is skewed to the white community, which is also the minority (Holborn & Eddy, 2011). Families live together for survival as most youths are not working in South Africa and therefore family income can depend on the old age grant and child support grant. Figure 1 also shows a lower number of fathers who are present in the lives of these students compared to mothers. In this context most of these students depend on a government grant that is about R300 per month (about US$21 per month). If these students are fortunate enough to have a grandparent, the income the home receives will be increased by R1100 per month (about US$72 per month).

Figure 2 shows that at the time of the research most of the students in this study were aged five years, followed by aged six years and a few aged four years. According to South Africa's admission policy, only five to six year old students are supposed to be in the Reception class. In these schools, the Reception class sizes exceeded 45 students (average 47), which represented severe overcrowding in a Reception class, compared with the policy target of student to teacher ratio 30:1 (DoBE, 2011). In these classrooms, students had only one teacher with no assistants.

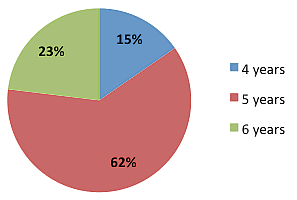
Figure 2

Figure 2: Reception class students' ages

As shown in Figure 3, no home had more than 10 books, and it is possible that the books that were there belonged to the schools, thus they were textbooks. The variables used in this graph are used in the TIMSS study to indicate how poor these homes are in the South African context. However, it is important to note that TV plays a significant role in developing students' language as they may spend most of their afternoons watching TV at home. As discussed in the findings below, these students' English language abilities develop prior to entering school, an indication of exposure to English language at home.

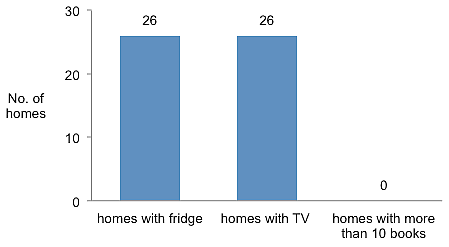
Figure 3

Figure 3: Students' home economic status

Thematic report

Mathematical literacy is English dominated

Of the 26 students, 12 demonstrated attainment of three developmental progressions in English, namely verbal counting, one-to-one correspondence, and cardinality.

From this group of 12 students, one of them (Student A) counted 55 counters accurately, moving each as she counted them and at the end reporting that the counters numbered 55. In her counting she used English number names. When the researcher asked this student if she could count the same counters in her home language (Xhosa), she shook her head. Then the researcher asked her to count starting from "inye", which means one in the Xhosa language. The student then started object counting in Xhosa as "inye, zimbini, zintathu, zine, zintlanu, ntandathu, sixhenxe, sibhozo, lithoba, lishumi" ending at 10. Then the researcher asked her to continue counting. The response from the student was "andikwazi", meaning "I cannot". This student was also able to write numerals from one to 20 as shown in Figure 4, though missing 16. Note in Figure 4 that 17 is written as a mirror image rather than the correct 17, indicating a need for more practice in writing the number 7, also 5 is challenging for this student, although in 15 it is correctly written.

Figure 4

Figure 4: Student A numeral writing

Eight of these students followed suit with lowest counting being to 29 and the highest to 49 in English, with all three developmental levels achieved. Five of these eight students also struggled to understand counting in Xhosa until the hint of "inye" from the researcher; they then counted in Xhosa to 10 doing object counting and stating the total number of counters at the end as 10. One of the students counted in both languages as "inye one, zimbini two, zintathu three, zine four, zintlanu five, ntandathu six, sixhenxe seven, sibhozo eight, lithoba nine, lishumi 10". The remaining three students showed different levels; one could not even attempt to count in Xhosa; the second one tried but counted to 10 in English; then the third one tried but was only able to count to three ("inye, zimbini, zintathu") object counting. Only two, Student B and C, of these eight students were also able to write numbers from one to 10. Below is the evidence of their number writing.

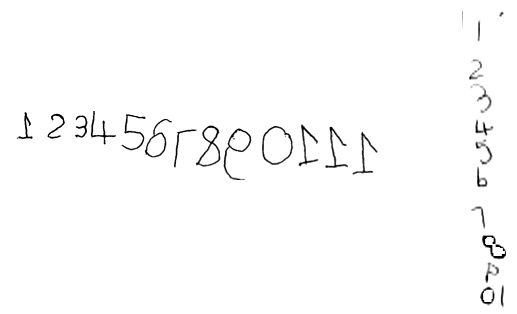Figures 5 and 6
Figure 5: Student B numeral writingFigure 6: Student C
numeral writing

The last three students were able to count from one to 23, with one student ending at 20 object counting. The two students were both able to count "ngo inye" meaning home language to 10 doing object counting and giving the total number of the 10 counters. One of these students, Student D, was able to write numbers from one to 10 and the other two were not able to write numbers. Below is evidence of the writing of one of the students.

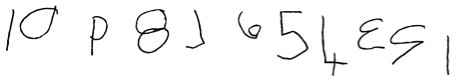
Figure 7

Figure 7: Student D numeral writing

Xhosa and English mathematical literacy sharing fluency

Eight students showed a balance between the two languages in their counting development. All eight students were able to do object counting and cardinality from one to 10, with a highest of 13 for two of them. Similarly, these students demonstrated the same level in their home language from "inye ukuya kwishumi" meaning one to 10. They also showed that they could respond accurately to the "how many" question. The eighth student could only count from one to 10 in the object counting and in the cardinality only in English. One of the eight students (when counting in home language) used both languages like "inye one, zimbini two, sintathu three, zine four, zintlanu five, ntandathu six, sixhenxe seven, sibhozo eight, lithoba nine, lishumi 10".

Only two of these students, Student E and F were able to write numbers. Others wrote alphabets, some zigzags and some only three numbers.

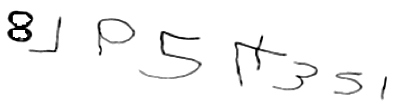
Figure 8

Figure 8: Student E numeral writing

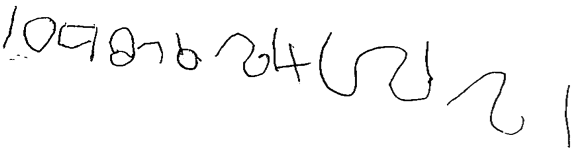
Figure 9

Figure 9: Student F numeral writing

Xhosa mathematics literacy leading

The last group of five students showed that their counting in English was poor, although when asked to count they used it without hesitation. All five students could not exceed six in object counting in English, and could not respond to the "how many" question in English. One of these students refused to count, as she mentioned "andikwazi kubala", meaning "I cannot count". However, when students were prompted by the researcher on the first Xhosa name for one, "inye", everything started to change. Three of these students counted from one to 10 in Xhosa, touching objects accurately. The other two were also doing the translating, counting in their object counting of "inye one, zimbini two, zintathu three, zine four, zintlanu five, ntandathu six, sixhenxe seven, sibhozo eight, lithoba nine, lishumi 10".

Discussion

The first part of the discussion responds to the first question of the study: (1) How advanced are Reception class students in terms of learning trajectories (Clements & Sarama, 2009) in using their home language for counting before entering formal schooling? It is clear from the findings that the students observed in this research enter Reception class with counting concepts that are meaningful and need to be extended (though the findings may not be widely generalisable). However, these concepts were not developed in their home language, but in English. The majority of these students demonstrated that they exceeded the minimum requirements of the CAPS curriculum of South Africa, which requires them to count meaningfully to 10, the minimum in the English language. The challenge with these findings is that the language policy requires use of home language exclusively in the Reception class. The students investigated in this research enter formal school with a different language tool than the expected. Vygotsky (1978) suggested that for new ideas to become meaningful and be owned, a student needs to connect the new ideas with his/her own existing ideas and cultural tools. In this case the home language is Xhosa, but the numeracy language the students have developed is English. The students who are emerging from this investigation challenge both the curriculum and the language policy.

The second question asks: (2) Does the developmental progression observed in home language mediate counting concepts further? According to the findings of this research, the Xhosa number counting does not exceed 10 and for many students their Xhosa counting levels ended at one-to-one correspondence in the developmental progression. Some students used English as their referral language for more meaningful counting. The English development shown by the students also led to numeral documentation. Literature which reveals that language proficiency in the language of teaching increases mathematics performance assists in understanding these findings (Alexander, 1999; Anthony & Setati, 2008; Ball, 2010; Cummins, 1996; Heugh, 2002; Skutnabb-Kangas, 2000). These young students, coming from low socio-economic home backgrounds, have been exposed to numeracy that is communicated in English rather than in their mother tongue. It is clear that only English numerals are used in their community, hence it was easy for them to develop further in the pre-schools they attended before school. This paper therefore challenges the understanding of the current literacies in research and policy-making level. If the school sticks with the current language policy in developing these students, what will it be creating if the student goes back to the community that uses English numeracy language? This paper calls for more research that is interdisciplinary in studying new emerging linguistic identities in young learners for their relevant mathematical development. The findings of the paper point to a number of misalignments between the emerging student and language policy, the emerging student and curriculum expectations, and the developing literacies and research.

Acknowledgement

I would like to acknowledge the National Research Foundation for funding this work. In addition I would like to acknowledge Ms N Njovane, and Mrs N Klass who were community assistants for the project, specifically for identifying teachers' and learners' needs within the school and classrooms. Dr Tlou and Ms N Bambiso who worked on their specific research interests in this project are also acknowledged for assisting in data collection.

References

Adler, J. (1998). A language of teaching dilemmas: Unlocking the complex multilingual secondary mathematics classroom. For the Learning of Mathematics, 18(1), 24-33. http://www.jstor.org/stable/40248258

Adler, J. (2001). Teaching mathematics in multilingual classrooms. Dordrecht: Kluwer.

Alexander, N. (1999). English unassailable but unattainable: The dilemma of language policy in South African education. PRAESA Occasional Papers, 3. Cape Town: PRAESA.

Anthony, E. & Setati, M. (2007). Exploring the English proficiency-mathematical proficiency relationship in learners: An investigation using instructional English computer software. In J. H. Woo, H. C. Lew, K. S. Park & D. Y. Seo, (Eds.), Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, 2, pp. 217-224. Seoul: PME. http://hdl.handle.net/10539/2019

Ball, J. (2010). Enhancing learning of children from diverse language backgrounds: Mother tongue-based bilingual or multilingual education in the early years. Geneva, Switzerland: UNESCO. http://unesdoc.unesco.org/images/0021/002122/212270e.pdf

Barwell, R. (2002). Understanding EAL issues in mathematics. In C. Leung (Ed.), Language and additional/second language issues for school education. (pp. 69-80). Watford: NALDIC. http://www.naldic.org.uk/eal-publications-resources/Shop/shop-products/b4.html

Bialystock, E. (2006). Bilingual in development: Language, literacy and cognition. Cambridge: Cambridge University Press.

Beal, C. R., Adams, N. M. & Cohen, P. R. (2010). Reading proficiency and mathematics problem solving by high school English language learners. Urban Education, 45(1), 58-74. http://dx.doi.org/10.1177/0042085909352143

Botes, H. & Mji, A. (2010). Language diversity in the mathematics classroom: Does a learner companion make a difference? South African Journal of Education, 30(1), 123-130. http://www.ajol.info/index.php/saje/article/view/52606

Brown, C. R., Cady, J. A. & Lubinski, C. A. (2011). The effects of poverty and language on mathematics achievement for English language learners. New York: Springer.

Carroll, J. B. (Ed.) (1997) [1956]. Language, thought, and reality: Selected writings of Benjamin Lee Whorf. Cambridge, Mass.: Technology Press of Massachusetts Institute of Technology. http://www.jstor.org/stable/j.ctt5hhbx2

Clements, D. H. & Sarama, J. (2009). Learning and teaching early math: The learning trajectories approach. New York: Routledge.

Clements, D. H. & Sarama, J. (2014). Learning and teaching early math: The learning trajectories approach (2nd edition). New York: Routledge.

Creswell, J. W. (2003). Research design: Qualitative, quantitative, and mixed methods approaches (2nd edition). California: SAGE.

Cummins, J. (1996). Negotiating identities: Education for empowerment. Covina: California Association for Bilingual Education.

Department of Education (1997). Language in education policy. http://www.education.gov.za/Resources/Policies.aspx [file LanguageEducationPolicy1997.pdf]

Department of Education (2002). Revised National Curriculum Statement Overview: Grades R-9. Pretoria: Government Printers. http://www.education.gov.za/Portals/0/CD/GET/doc/overview.pdf?ver=2006-11-21-100143-000

Department of Basic Education (2011). Universal Access to Grade R: Policy Framework. http://www.thutong.doe.gov.za/ResourceDownload.aspx?id=47575&userid=-1

Department of Basic Education (2014). National Curriculum Statement: Curriculum Assessment Policy. Foundation Phase Grades R to 3. http://www.education.gov.za/LinkClick.aspx?fileticket=%2BrzCcDZUb5k%3D&tabid

Essien, A. A. & Setati, M. (2007). Exploring the English proficiency-mathematical proficiency relationship in learners: An investigation using instructional English computer software. In J. H. Woo, H. C. Lew, K. S. Park & D. Y. Seo (Eds.), Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, 2, 217-224. Seoul: PME. [see http://wiredspace.wits.ac.za/handle/10539/2019]

Feza-Piyose, N. (2012). Language - a cultural capital for conceptualizing mathematics knowledge. International Electronic Journal of Mathematics Education, 7(2), 62-79. http://iejme.com/makale/288

Feza, N. N. (2013). Inequities and lack of professionalisation of early childhood development practice hinder opportunities for mathematics stimulation and realisation of South African policy on quality education for all. International Journal of Inclusive Education, 18(9), 888-902. http://dx.doi.org/10.1080/13603116.2013.855266

Feza, N. N. (2015). Teaching 5- and 6-year-olds to count: Knowledge of South African educators. Early Childhood Education Journal, 44(5), 483-489. http://dx.doi.org/10.1007/s10643-015-0736-z

Henry, D. L., Baltes, B. & Nistor, N. (2014). Examining the relationship between math scores and English language proficiency. Journal of Educational Research and Practice, 4(1), 11-29. http://scholarworks.waldenu.edu/jerap/vol4/iss1/2/

Heugh, K. (2012). The case against bilingual and multilingual education in South Africa. Occasional Paper 6: PRAESA. http://www.praesa.org.za/files/2012/07/Paper6.pdf

Kieffer, M. J., Lesaux, N. K., Rivera, M. & Francis, D. J. (2009). Accommodations for English language learners taking large scale assessments: A meta-analysis on effectiveness and validity. Review of Educational Research, 79(3), 1168-1202. http://dx.doi.org/10.3102/0034654309332490

Klass, A. & Trudell, B. (2011). Effective literacy programmes and independent reading in African contexts. Language Matters, 42(1), 22-38. http://dx.doi.org/10.1080/10228195.2011.569739

Mbatha, T. (2014). Experiences of foundation phase teachers qualified in a dual medium programme. Per Linguam, 30(2), 37-50. http://dx.doi.org/10.5785/30-2-564

Mullis, I. V. S., Martin, M. O., Foy, P. & Drucker, K. T. (2012). PIRLS 2011 International Results in Reading. TIMSS & PIRLS International Study Center: Lynch School of Education Boston College. http://timssandpirls.bc.edu/pirls2011/international-results-pirls.html

Nunan, D. (2003). The impact of English as a global language on educational policies and practices in the Asia-Pacific region. TESOL Quarterly, 37(4), 589-613. http://dx.doi.org/10.2307/3588214

Salehmohamed, A. & Rowland, T. (2014). Whole-class interactions and code-switching in secondary mathematics teaching in Mauritius. Mathematics Education Research Journal, 26(3), 555-577. http://dx.doi.org/10.1007/s13394-013-0103-6

Selamat, J. T. (2014). Code switching in the Malaysian ESL classroom. Unpublished Master of Arts thesis, University of Otago. http://hdl.handle.net/10523/4909

Setati, M. & Adler, J. (2001). Between languages and discourses: Language practices in primary multilingual mathematics classrooms in South Africa. Educational Studies in Mathematics, 43(3), 243-269. http://dx.doi.org/10.1023/A:1011996002062

Setati, M. (2005). Mathematics education and language: Policy, research and practice in multilingual South Africa. In R. Vithal, J. Adler & C. Keifel (Eds.), Researching mathematics education in South Africa: Perspectives, practices and possibilities. Cape Town: HSRC Press.

Setati, M. (2008). Access to mathematics versus access to the language of power: The struggle in multilingual mathematics classrooms. South African Journal of Education, 28(1), 103-116. http://www.sajournalofeducation.co.za/index.php/saje/article/view/150/99

Skutnabb-Kangas, T. (2000). Linguistic genocide in education -- or worldwide diversity and human rights? London: Taylor & Francis.

Spaull, N. & Kotze, J. (2014). Starting behind and staying behind in South Africa: The case of insurmountable learning deficits in mathematics. Stellenbosch Economic Working Papers. http://www.ekon.sun.ac.za/wpapers/2014/wp272014/wp-27-2014.pdf

Vygotsky, L. (1978). Mind in society: The development of higher psychological process. Cambridge, MA: Harvard University Press.

Winsor, M. S. (2007). Bridging the language barrier in mathematics. Mathematics Teacher, 101(5), 372-378. http://eric.ed.gov/?id=EJ781012

Author: Nosisi Nellie Feza is an Associate Professor in the College of Graduate Studies, University of South Africa, where she is a Head of the Institute for Science and Technology Education. She has obtained a PhD in Mathematics Education from the State University of New York at Buffalo, New York as a Fulbright scholar. She received a Diversity Scholar Award from the National Center for Institutional Diversity in Michigan in 2009. Her research interests are early childhood mathematics stimulation and teacher development and cultural influence in learning mathematics in students of African descent.
Email: fezann@unisa.ac.za
Websites: http://www.unisa.ac.za/default.asp?Cmd=ViewContent&ContentID=97778
https://sites.google.com/site/nosisifeza/classroom-news

Please cite as: Feza, N. N. (2016). Basic numeracy abilities of Xhosa Reception year students in South Africa: Language policy issues. Issues in Educational Research, 26(4), 576-591. http://www.iier.org.au/iier26/feza.html

[ PDF version of this article ] [ Contents Vol 26 ] [ IIER Home ]
This URL: http://www.iier.org.au/iier26/feza.html
Created 25 Oct 2016. Last revision: 25 Oct 2016.
HTML: Roger Atkinson [rjatkinson@bigpond.com]