Self-perceptions of pre-service mathematics teachers completing a Graduate Diploma of Secondary Education

Gregory S. C. Hine
The University of Notre Dame Australia

This qualitative research project explored the self-perceptions of pre-service secondary mathematics teachers completing a Graduate Diploma of Secondary Education. Specifically, the researcher investigated the extent to which teachers perceived their readiness to commence a secondary mathematics teaching position. The project relied principally on the use of a single, 10-item, qualitative research instrument that was used repeatedly and flexibly over time. Participants were asked to complete two questionnaires; one was administered before and after their Teaching Internship Practicum. Responses from all participants indicated varying degrees of readiness to teach secondary mathematics. An analysis of participant responses suggests three key findings: pre-service teachers require further training in mathematical content, particularly in upper school content; pre-service teachers require additional training in mathematical pedagogy; and the practicum experience confirmed initial participant perceptions of teaching readiness.

Introduction

Purpose of the research

Review of literature

Mathematical content

Highly effective teachers have a deep understanding of the subjects they teach. These teachers have studied the content they teach in considerably greater depth than the level at which they currently teach and they have high levels of confidence in the subjects they teach. Their deep content knowledge allows them to focus on teaching underlying methods, concepts, principles and big ideas in a subject, rather than on factual and procedural knowledge alone (p. 4).

Despite a strong emphasis placed on pre-service teachers' acquisition of mathematical content knowledge, the link between teachers' background knowledge and their students' achievement is at best only mildly positive (Miller & Davison, 2006). To amplify, Ball (1990) found that prospective secondary mathematics teachers had only a cursory understanding of the concepts underlying elementary mathematics. In general, there appears to be no association between the number of advanced mathematics courses a teacher takes and how well his/her students achieve in mathematics (Monk, 1994). Ma (1999) discovered that Chinese teachers, even though they had less formal instruction in mathematics than American teachers, had more profound knowledge of basic mathematics and worked harder at developing effective ways to teach. Several decades ago, Begle (1979) asserted:

It is widely believed that the more a teacher knows about his subject matter, the more effective he will be as a teacher. The empirical literature suggests that this belief needs drastic modification and in fact suggests that once a teacher reaches a certain level of understanding of the subject matter, then further understanding contributes nothing to student achievement. (p. 51).

Mathematical pedagogy

Various commentators herald the importance of reinforcing theory and practice within teacher-education programs (Emerick et al., 2003; Miller & Davidson, 2006; TEMAG, 2014). For instance, the TEMAG (2014, p. xiii) asserted that pre-service teachers must develop a "solid understanding of teaching practices that are proven to make a difference to student learning". Furthermore, Emerick et al. (2003) argued that high quality teachers must possess both appropriate content knowledge and an ability to communicate effectively to students. Miller and Davidson articulated this claim, stating that "teacher dispositions like collegiality, self-reflection, collaborative and interactive skills, and the ability to adjust personal and professional practice based on reflection are important characteristics of good teachers" (2006, p. 58). Pre-service teachers often begin teacher education programs with strongly held beliefs about teaching and learning (Cavanagh & Garvey, 2012). Their own school experiences exert a powerful influence on their conceptions about the curriculum and how best to teach it, and they invariably want to teach as they were taught (Sherrf & Singer, 2012). This is a critical issue in secondary mathematics because most pre-service teachers have themselves learned mathematics in a traditional manner (Ebby, 2000). Consequently, pre-service teachers are unfamiliar with alternative pedagogical approaches and tend to want to teach very teacher-centred lessons. The situation is exacerbated because rather than challenge pre-service teachers' prior understandings, some teacher education courses and field experiences have been found to reinforce them (Zeichner, 2010).

Practicum experience

From their own research, Cavanagh and Prescott (2007) reported that the student-teachers' own secondary school experiences bore close resemblances to their practicum observations. As such, these practicum observations served to reinforce this style of teaching as an acceptable and workable model of pedagogy (Cavanagh & Prescott). Wubbels et al. (1997) referred to a didactic teaching-learning-teaching cycle in which teacher education programs did not provide pre-service teachers with opportunities to critically analyse their own schooling. In a similar vein, Chamoso et al. (2012) posited that one crucial element in helping prospective teachers identify some of the shortcomings in traditional teaching practices, and encouraging them to broaden their range of pedagogical approaches, is by engaging in critical reflection on the lessons they observe and teach. In addition, professional experience placements may not provide pre-service teachers with opportunities to observe or teach using student-centred approaches (Cavanagh & Garvey, 2012). Consequently, pre-service teachers may simply replicate the kinds of teaching they received in their own schooling without carefully considering alternative approaches (Eames & Coll, 2010). Eames and Coll (2010) exhorted teacher educators to devise new kinds of professional experience programs that help pre-service teachers integrate theory and practice. These authors suggested that pre-service teachers be given multiple opportunities to experiment with novel teaching approaches different from those they experienced when they were students themselves. In doing so, pre-service teachers may be better able to appreciate the importance of a variety of mathematics pedagogies and reframe their ideas about what constitutes quality learning and teaching (Star & Strickland, 2008).

Methodology

Methods

Research context

Within the unit, students complete two assessments: A Forward Planning Document (FPD) and a Practicum Reflective Workbook (PRW). The FPD is comprised of twelve sequential, well-detailed lessons of a particular theme or unit of work in mathematics. Additionally, one lesson from the FPD must be written up in considerable detail and using a Lesson Plan template. The PRW requires pre-service teachers to record observations and reflect upon pedagogical experiences while on a two-week Classroom Immersion Period. Following the annotation of these observations and experiences, pre-service teachers respond to a series of reflective questions regarding mathematical content, mathematical pedagogy, technology, resources, and classroom management. These assessments meet the program standards for initial teacher education programs in Australia. During contact hours, pre-service teachers engage with secondary mathematical pedagogy (both for lower school and upper school students), examine key curriculum and policy documents, and investigate best practice approaches regarding planning, assessment, technology, and resources.

Sample

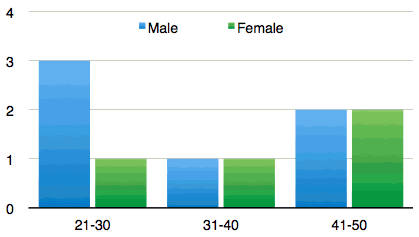
Figure 1: Age of participants

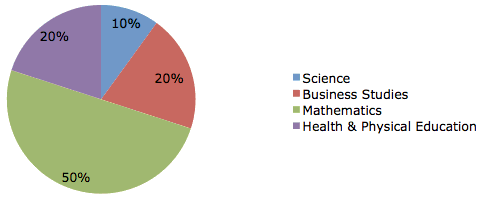
Figure 2: Undergraduate major of participants

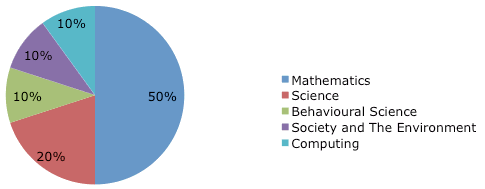
Figure 3: Undergraduate minor of participants

Survey items

1. What is your gender?
2. What is your major teaching area?
3. What is your specialisation teaching area?
4. Which category below includes your age?
5. Describe your readiness to teach secondary mathematics students in terms of the mathematical content knowledge and skills you currently possess.
6. In what area(s) of mathematical content knowledge do you feel you require further training?
7. Describe your readiness to teach secondary mathematics students in terms of the mathematical pedagogical knowledge and skills you currently possess.
8. In what area(s) of mathematical pedagogical knowledge do you feel you require further training?
9. As a pre-service, secondary mathematics educator, are there any other areas you would like to receive professional training and development in?
10. Overall, describe your readiness to teach mathematics to secondary students.

Data analysis process

Findings

Mathematical content knowledge - readiness

I am only now studying the highest level of mathematics that is taught in secondary schools. There are many gaps in my content knowledge, especially in topics that were covered when I was in Year 10-11 and not a very serious student, and also in topics which are not continuously emphasised throughout the school curriculum (such as project networks and some topics in statistics). However I was able to re-learn much of this in detail so that I could teach it during prac[ticum].

Immediately following the 12-week practicum experience, all of the participants (10 of 10) averred their preparedness to teach secondary school mathematics. This time, three of ten participants intimated a readiness to teach mathematics only to lower school students. Another three of ten participants voiced that 'gaps' in content knowledge would restrict them in teaching upper school mathematics courses. For example, one pre-service teacher stated "I have appropriate content knowledge for lower secondary and basic classes in upper secondary. More work is needed to prepare for the likelihood of teaching advanced class in upper secondary." Additionally, a number of participants (3 of 10) stated that 'gaps' in content knowledge that would restrict them in teaching specialist mathematics courses. One pre-service teacher commented "Lower school [content] is good. Some upper school skills require refresh[ing], but overall I am very ready to teach maths to secondary students up to 3C-3D." The most commonly reported self-perceptions of mathematical teachers' content knowledge are shown in Table 1.

Pre-practicum	Relative frequency	Post-practicum	Relative frequency
Prepared	10 of 10	Prepared	10 of 10
Prepared (lower school)	4 of 10	Prepared (lower school)	3 of 10
Prepared (upper school gaps)	4 of 10	Prepared (upper school gaps)	3 of 10
Prepared (specialist gaps)	4 of 10	Prepared (specialist gaps)	3 of 10

Mathematical content knowledge: Further training needed

It would be good if there were one of two units earlier in my course which cover upper school mathematics in such a way that I could fill in any gaps in my knowledge about the maths that I now need to teach. I can learn this [content] as I teach but I would feel more prepared if I had some more training beforehand.

After the practicum experience, a majority of participants (6 out of 10) maintained that there were areas of their mathematical content knowledge that required further training. Specifically, participants avowed that they required further training in upper school content (4), specialist content (4), and general content (2). Again, participants expressed particular mathematical topics required for their own professional learning such as: geometry, differential and integral calculus, trigonometry, probability, quadratics, matrices. After observing upper school lessons on practicum, one participant stressed that she needed support in the content taught in WACE Courses of Study 3A-3D. Four participants stated that they did not need any further training in mathematical content. The most commonly proffered responses for further mathematical training needed by pre-service teachers are displayed in Table 2.

Pre-practicum	Relative frequency	Post-practicum	Relative frequency
Upper school content	5 of 10	Upper school content	4 of 10
Specialist content	4 of 10	Specialist content	4 of 10
General content	4 of 10	None	4 of 10
None	2 of 10	General content	2 of 10

Mathematical pedagogical knowledge: Readiness

I feel I have all the skills (from a pedagogical perspective) because the pedagogical knowledge was dealt with so comprehensively. I particularly valued the shift to teaching mathematics in the context of real life examples (e.g. exploratory) and using student centred [lessons] rather than teacher [centred lessons].

I know a lot of pedagogical theories that I will take into account when planning lessons and teaching, but in practice I can only integrate a few of them into my lessons. I do feel well prepared in terms of general pedagogical knowledge, and I'm looking forward to developing my pedagogical knowledge that is specific to teaching mathematics.

Following the practicum experience, all participants (10 of 10) reaffirmed they possessed sufficient pedagogical knowledge to teach secondary mathematics. One pre-service teacher explained how the practicum experience had helped him consolidate his pedagogical knowledge, in that "My skills are relatively strong, [and I] need more repetitiveness so that they become habits. I have picked up many different things to engage with the students and motivate their learning." A majority of the participants (7 of 10) acknowledged that despite acquiring sufficient pedagogical knowledge to teach secondary mathematics, they wished to develop their pedagogical skills further. For example, one pre-service teacher stated "I am very ready to successfully apply what I have already learned, and my pedagogical skills are constantly growing and evolving. I will need to find a range of ways to develop my skills and to learn more about how to better teach mathematics." A number of participants offered that they felt confident to apply general pedagogy within secondary mathematics classes (5 of 10), while others disclosed that they required further professional training in using inclusive pedagogical approaches (2 of 10). In contrast to pre-practicum comments, no participants acknowledged a lack of confidence due to teaching inexperience. Participants' responses regarding mathematical pedagogical knowledge are shown in Table 3.

Pre-practicum	Relative frequency	Post-practicum	Relative frequency
Prepared	10 of 10	Prepared	10 of 10
General pedagogy	6 of 10	Prepared and developing	7 of 10
Lower school pedagogy	3 of 10	General pedagogy	5 of 10
Upper school pedagogy	2 of 10	Inclusive pedagogy needed	2 of 10

Mathematical pedagogical knowledge: Further training needed

I have learned a lot about Bloom's Taxonomy, constructivism and other broad theories but very little about specific ways of teaching maths. Being creative and observing other teachers' own techniques are both important but I would feel better prepared to teach mathematics if I could learn more about specific strategies that have been found to be effective when used properly. This sort of information helps me to better evaluate my own ideas and the teaching strategies that I observe.

After the practicum experience, a majority of participants (6 of 10) indicated that they required further training in general pedagogy. Five participants mentioned that they needed additional preparation in mathematical pedagogy. A range of statements regarding general pedagogy included a need to "create a learning environment in which every student is engaged", "learn a few different teaching style ideas, but nothing too major", and "watch other teachers teach maths and sharing notes with them." Four participants reported that they did not require any further training concerning mathematical pedagogical knowledge. A number of participants (4 of 10) reflected that they needed supplementary training in lower school pedagogy. One pre-service teacher delineated her professional development needs by stating:

I want to learn how to break down the simple stuff. I am finding when teaching Year 7/8 I assume too much. Many [students] do not know their times tables and so simplifying fractions becomes difficult. Techniques for scaffolding these gaps would be great.

Pre-practicum	Relative frequency	Post-practicum	Relative frequency
General pedagogy	5 of 10	General pedagogy	6 of 10
Mathematical pedagogy	3 of 10	Mathematical pedagogy	5 of 10
No training needed	2 of 10	No training needed	4 of 10
Lower school pedagogy	2 of 10	Lower school pedagogy	4 of 10

Further professional development

Pre-practicum	Relative frequency	Post-practicum	Relative frequency
Graphics calculators	3 of 10	Graphics calculators	5 of 10
General content	3 of 10	General content	4 of 10
Resources	2 of 10	Classroom management	2 of 10
Assessments	2 of 10	Special needs education	2 of 10

Overall readiness to teach mathematics

Following the practicum experience, all participants (10 of 10) affirmed that they were prepared to teach secondary mathematics. Again, participant responses concerning their self-perceived degree of readiness were geared towards year level and the mathematical content. The most commonly offered responses comprised participants asserting their readiness to teach all content from Years 7-12 (but not specialist mathematics) (6 of 10), and asserting their readiness to engage with mathematics pedagogy from Years 7-12 (but not specialist mathematics) (6 of 10). Four participants also expressed confidence to teach all content from Years 7-12 (including specialist mathematics). Additionally, four participants shared that they felt prepared to teach lower school classes only. Participants' responses regarding their overall readiness to teach secondary mathematics are displayed in Table 6.

Pre-practicum	Relative frequency	Post-practicum	Relative frequency
Prepared (lower school)	5 of 10	Prepared (general content)	6 of 10
Prepared (general content)	4 of 10	Prepared (general pedagogy)	6 of 10
Prepared (specialist content)	3 of 10	Prepared (specialist content)	4 of 10
Prepared (general pedagogy)	3 of 10	Prepared (lower school)	4 of 10

Discussion

All pre-service teachers (10 of 10) avowed their readiness to teach secondary mathematics in terms of content knowledge and skills to varying degrees. However, and before the practicum experience, only 4 of 10 pre-service teachers stated a readiness to teach only lower school (Years 7-10) mathematics courses. Following the practicum this number was reduced to 3 of 10. Similar numbers represented participants' self-perceptions that 'gaps' in upper school content (4 of 10 before; 3 of 10 after) and specialist content (4 of 10 before; 3 of 10 after) would restrict their ability to teach those respective courses of study. When pre-service teachers were asked to identify areas of content requiring further training, the most popular responses included upper school content (5 of 10 before; 4 of 10 after) and specialist content (4 of 10 before; 4 of 10 after). Concerning further professional development, pre-service teachers expressed a need to engage in mathematical content 'refresher' courses prior to teaching (3 of 10 before; 4 of 10 after). When describing their overall readiness, 4 of 10 pre-service teachers expressed confidence teaching all content from Years 7-12 (but not specialist mathematics) before the practicum experience; following the practicum this number grew to 6 of 10. Additionally, fewer than half pre-service teachers (3 of 10 before; 4 of 10 after) described their readiness to teach all content from Years 7-12 (including specialist mathematics).

All pre-service teachers (10 of 10) asserted their readiness to teach secondary mathematics in terms of pedagogical knowledge and skills to varying degrees. For instance, a number of pre-service teachers mentioned they required further training in general pedagogy (6 of 10 before practicum; 5 of 10 after practicum). Following the practicum experience, 7 of 10 participants acknowledged that despite acquiring sufficient pedagogical knowledge to teach secondary mathematics, they wished to further develop their pedagogical acumen. When asked to identify pedagogical training opportunities, pre-service teachers mentioned they required more training in general pedagogy (5 of 10 before; 6 of 10 after) and in mathematical pedagogy (3 of 10 before; 5 of 10 after). A need to engage in further professional development concerning graphics calculators was strongly voiced by pre-service teachers (3 of 10 before; 5 of 10 after). Furthermore, in describing their overall readiness pre-service teachers (3 of 10 before; 6 of 10 after) stated they felt prepared to engage with mathematical pedagogy needed in Years 7-12 (but not specialist mathematics).

To a large extent, the practicum experience confirmed participants' initial perceptions of teaching readiness regarding mathematical content and pedagogy. To illustrate, there was very little change in participants' pre-practicum responses and post-practicum responses (see Tables 1-6). While an examination of the practicum experience was not an explicit focus of the research per se, participants offered various comments to suggest that the ten-week internship was valuable in their preparation as secondary mathematics teachers. For instance, the practicum experience was an opportunity for pre-service teachers to learn mathematics content and mathematics pedagogy from mentor teachers. It served as a period where mentors' teaching styles and methods of creating a mathematical learning environment could be discerned. The experience enabled pre-service teachers both to implement teaching strategies learnt in the Graduate Diploma of Secondary Education, and to experiment with methods dissimilar to those from their own mathematical education. Finally, the practicum experience assisted pre-service teachers with the identification and confirmation of mathematical content and pedagogy required for personal, professional development.

Testimony from participants clearly indicated they required additional training in mathematical content before assuming a secondary teaching position (Cannon, 1997; Norton, 2010). Specifically, topics and concepts from upper school mathematics courses were frequently referred to as 'gaps' in mathematical knowledge. Although these participants recollected having learnt those particular topics and concepts in their undergraduate degree, it was clearly acknowledged that learning the content at a deeper level was essential before confidently teaching it to students (Masters, 2009; Silvernam & Thomson, 2008; U.S. Department of Education, 2008). This is a particularly interesting finding, as students enrolling into the Graduate Diploma of Secondary Education must have completed eight tertiary mathematics units for a teaching major in mathematics, or four tertiary mathematics units for a mathematics specialisation. Two possible explanations are offered to account for these apparent knowledge 'gaps'. First, 6 of 10 participants were older than 30 years of age, and would have completed their undergraduate degree approximately a decade ago. Second, topics and concepts in mathematical syllabi have changed several times over the last ten years; as such, participants would not have engaged with some content during their undergraduate studies. Participants also highlighted the need for further training in mathematical pedagogy. Together with additional opportunities to learn mathematical content, pre-service teachers saw the development of their own subject knowledge and pedagogical knowledge as critical for successful learning outcomes (Chick, 2012; Shulman, 1987, 1999). Comments from pre-service teachers also indicated a need to "try different things", "use interesting lessons", and "finding specific strategies that work" in clearly communicating mathematical concepts to students (Emerick et al., 2003; Miller & Davidson, 2006). Through observing their mentors' teaching styles, implementing theoretical models learnt at university (Shane, 2002), and using a variety of lessons (Star & Strickland, 2008), pre-service teachers saw the practicum experience as valuable to their engagement with mathematical content and pedagogy (Eames & Coll, 2020; Putnam & Borko, 2000).

Limitations and implications for further research

This research may be replicated and developed further by other researchers interested in secondary mathematics teacher education. Considerations for further research could include developing a two-year, longitudinal study to assess the extent to which pre-service secondary mathematics teachers feel their tertiary training was useful. Data gathered from such a project could offer insight as to the perceived value of teacher education programs both during tertiary training and the first year of professional appointment. A larger-scale project conducted across multiple tertiary institutions (at state and national levels) could provide valuable information outlining the efficacy of current efforts in preparing secondary mathematics teachers. It may also be practicable to relate participants' self-perceptions to their academic grades (including their Teaching Internship grade) achieved within the Graduate Diploma of Secondary Education

Conclusion and recommendations

Second, it is recommended that school leaders remain cognisant and supportive of the professional needs of beginning mathematics teachers. To illustrate, certain needs can be met through the exercise of mentorship and induction programs, as well as offering 'release time' for beginning teachers to engage in professional learning opportunities.

Third, the author will use the proffered insights of student participants to strengthen future offerings of the unit EDSM04/EDSS04: Secondary Teaching Method (Mathematics). Tangential to this third recommendation is an opportunity for teacher educators to consider the content of their own tertiary units against the needs of their pre-service mathematics teachers. In light of the findings of this research and building upon the existing literature associated with this genre, these recommendations are aimed at teachers developing a profound mathematical knowledge for teaching (Silvernam & Thomson, 2008).

References

Artzt, A., Sultan, A., Curcio, F. R. & Gurl, T. (2011). A capstone mathematics course for prospective secondary mathematics teachers. Journal of Mathematics Teacher Education, 15(3), 251-262. http://dx.doi.org/10.1007/s10857-011-9189-5

Ball, D. L. (1990). The mathematical understandings that prospective teachers bring to teacher education. Elementary School Journal, 90(4), 449-466. http://www.jstor.org/stable/1001941

Ball, D. L., Hill, H. & Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, 29(1), pp. 14-46. http://hdl.handle.net/2027.42/65072

Banner, J. & Cannon, H. (1997). The elements of teaching. New Haven: Yale University Press.

Begle, E. G. (1979). Critical variables in mathematics education: Findings from a survey of empirical literature. Washington, DC: Mathematical Association of America/National Council of Teachers of Mathematics.

Boyd, D., Grossman, P., Lankford, H., Loeb, S. & Wyckoff, J. (2009). Teacher preparation and student achievement. Educational Evaluation and Policy Analysis, 31(4), 416-440. http://dx.doi.org/10.3102/0162373709353129

Cavanagh, S. (2009). Majoring in math not always a classroom plus. Education Week, 29(13), 14-15. http://www.edweek.org/ew/articles/2009/11/25/13mathteach.h29.html

Cavanagh, M. S. & Garvey, T. (2012). A professional experience learning community for pre-service secondary mathematics teachers. Australian Journal of Teacher Education, 37(12), 57-74. http://dx.doi.org/10.14221/ajte.2012v37n12.4

Cavanagh, M. & Prescott, A. (2007). Professional experience in learning to teach secondary mathematics: Incorporating pre-service teachers into a community of practice. In Proceedings Mathematics Educational Research Group of Australasia Conference. Mathematics: Essential Research, Essential Practice, 1, pp.182-191. http://hdl.handle.net/10453/7476

Chamoso, J. M., Caceres, M. J. & Azcarate, P. (2012). Reflection on the teaching-learning process in the initial training of teachers. Characterization of the issues on which pre-service mathematics teachers reflect. Teaching and Teacher Education, 28(2), 154-164. http://dx.doi.org/10.1016/j.tate.2011.08.003

Chick, H. (2012). Pedagogical content knowledge. Paper presented at CEMENT Conference. The University of Tasmania: Launceston.

Conference Board of the Mathematical Sciences (CBMS) (2012). The mathematical education of teachers II. Providence RI and Washington DC: American Mathematical Society and Mathematical Association of America. http://www.cbmsweb.org/MET2/index.htm

Cox, D. C., Chelser, J., Beisiegel, M., Kenney, R., Newton, J. & Stone, J. (2013). The status of capstone courses for pre-service secondary mathematics teachers. Issues in the Undergraduate Mathematics Preparation of School Teachers, 4, 1-10. http://www.k-12prep.math.ttu.edu/journal/4.curriculum/beisiegel01/article.pdf

Crotty, M. (1998). The foundations of social research: Meaning and perspective in the research process. Crows Nest: Allen & Unwin.

Darling-Hammond, L. (1997). Doing what matters most: Investing in quality teaching. National Commission on Teaching and America's Future. New York: National Commission on Teaching and America's Future. http://nctaf.org/wp-content/uploads/DoingWhatMattersMost.pdf

Eames, C. & Coll, R. K. (2010). Cooperative education: Integrating classroom and workplace learning. In S. Billett (Ed.), Learning through practice (pp. 180-196). Dordrecht: Springer. http://dx.doi.org/10.1007/978-90-481-3939-2_10

Ebby, C. B. (2000). Learning to teach mathematics differently: The interaction between coursework and fieldwork for preservice teachers. Journal of Mathematics Teacher Education, 3(1), 69-97. http://dx.doi.org/10.1023/A:1009969527157

Emerick, S., Hirsch, E. & Berry, B. (2003). Unfulfilled promise: Ensuring high quality teachers for our nation's students. http://www.teachingquality.org/content/unfulfilled-promise-ensuring-high-quality-teachers-our-nations-students-extensive-findings

Goos, M. E. (2006). License to thrill or live and let die? Principal Matters, Spring, 6-8.

Harris, K-L. & Jensz, F. (2006). The preparation of mathematics teachers in Australia: Meeting the demand for suitably qualified mathematics teachers in secondary schools. The University of Melbourne. http://cshe.unimelb.edu.au/research/disciplines/docs/Prep_Math_Teach_Aust.pdf

Loe, M. & Rezak, H. (2006). Creating and implementing a capstone course for future secondary mathematics teachers. Mathematicians and Education Reform Newsletter, 16(2), 8-11.

Ma, L. (1999). Knowing and teaching elementary mathematics: Teachers' understanding of fundamental mathematics in China and the United States. Mahawah, NJ: Lawrence Erlbaum Associates, Inc.

Masters, G. N. (2009). A shared challenge: Improving literacy, numeracy and science learning in Queensland primary schools. Camberwell, Victoria: Australian Council for Educational Research. http://education.qld.gov.au/mastersreview/pdfs/final-report-masters.pdf

Miles, M. B. & Huberman, M. A. (1994). Qualitative data analysis: An expanded sourcebook. Thousand Oaks, CA: SAGE.

Miller, K. W. & Davidson, D. M. (2006). What makes a secondary school science and/or mathematics teacher "highly qualified"? Science Educator, 15(1), 56-59. http://files.eric.ed.gov/fulltext/EJ773254.pdf

Ministerial Council on Education, Employment, Training and Youth Affairs (MCEETYA) (2008). National assessment program, literacy and numeracy: Numeracy. Carlton, Victoria: Curriculum Corporation.

Monk, D. H. (1994). Subject area preparation of secondary mathematics and science teachers and school achievement. Economics of Education Review, 13(2), 125-145. http://dx.doi.org/10.1016/0272-7757(94)90003-5

Moriarty, B. (2014). Research design and the predictive power of measures of self-efficacy. Issues in Educational Research, 24(1), 55-66. http://www.iier.org.au/iier24/moriarty.pdf

Norton, S. (2010). How deeply and how well? How ready to teach mathematics after a one-year program? Mathematics Education and Special Education, 12(1), 65-84. http://www.merga.net.au/ojs/index.php/mted/article/view/61/39

Osana, P., Lacroix, G., Tucker, B. & Desrosiers, C. (2006). The role of content knowledge and problem features on preservice teachers' appraisal of elementary mathematics tasks. Journal of Mathematics Teacher Education, 9(4), 347-380. http://dx.doi.org/10.1007/s10857-006-4084-1

Putnam, R.T. & Borko, H. (2000). What do new views of knowledge and thinking have to say about research on teacher learning? Educational Researcher, 29(1), 4-15. http://dx.doi.org/10.3102/0013189X029001004

Scherrf, L. & Singer, N. R. (2012). The preservice teachers are watching: Framing and reframing the field experience. Teaching and Teacher Education, 28(2), 263-272. http://dx.doi.org/10.1016/j.tate.2011.10.003

Shane, R. (2002). Context and content: What are pre-service teachers learning about teaching mathematics? In S. Goodchild & L. English (Eds.), Researching mathematics classrooms: A critical examination of methodology (pp. 119-154). Westport, Connecticut: Praeger.

Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-22. http://hepg.org/her-home/issues/harvard-educational-review-volume-57,-issue-1/herarticle/foundations-of-the-new-reform_461

Shulman, L. S. (1999). Knowledge and teaching: Foundations of the new reform. In J. Leach & B. Moon (Eds.), Learners and pedagogy (pp. 61-77). London: SAGE.

Silvernam, J. & Thompson, P. (2008). Toward a framework for the development of teachers. In F. K. Lester (Ed.), Second handbook of research on mathematics learning and teaching (pp. 157-224). Charlotte, NC: NCTM.

Star, J. R. & Strickland, S.K. (2008). Learning to observe: Using video to improve preservice mathematics teachers' ability to notice. Journal of Mathematics Teacher Education, 11(2), 107-125. http://dx.doi.org/10.1007/s10857-007-9063-7

Teacher Education Ministerial Advisory Group (2014). Action now: Classroom ready teachers. http://www.studentsfirst.gov.au/teacher-education-ministerial-advisory-group

U.S. Department of Education (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. http://www2.ed.gov/about/bdscomm/list/mathpanel/report/final-report.pdf

Wubbels, T., Kortahgen, F. & Broekman, H. (1997). Preparing teachers for realistic mathematics education. Educational Studies in Mathematics, 32(1), 1-28. http://dx.doi.org/10.1023/A:1002900522457

Zeichner, K. (2010). Rethinking connections between campus courses and field experiences in college- and university-based teacher education. Journal of Teacher Education, 61(1-2), 89-99. http://dx.doi.org/10.1177/0022487109347671

Authors: Gregory S. C. Hine PhD is a senior lecturer in the School of Education, The University of Notre Dame Australia. Greg lectures in general pedagogy, middle school and secondary mathematics, and educational action research. His areas of scholarly interest are student leadership, mathematics pedagogy and content, and educational action research. Email: gregory.hine@nd.edu.au Web: https://www.nd.edu.au/fremantle/schools/education/staff/ghine.shtml Please cite as: Hine, G. S. C. (2015). Self-perceptions of pre-service mathematics teachers completing a Graduate Diploma of Secondary Education. Issues in Educational Research, 25(4), 480-500. http://www.iier.org.au/iier25/hine.html