Measuring contextual error in the diagnosis of alternative conceptions in science
David H. Palmer
The University of Newcastle
A considerable amount of research in science education has focussed on the identification of students' alternative conceptions in the topic of forces and motion, and one important finding has been that students' responses to questions may vary according to contextual features such as the type or size of the moving body (factors which a scientist would consider to be irrelevant). If students' responses are contextually dependent in this way then it might be assumed that a "contextual error" could occur in the diagnosis of students' conceptions. For example, each diagnostic question has a specific context, so an individual's response to a single item might not be typical of their thinking about the topic overall. The present paper investigates the extent to which this is in fact the case.
Over the last two decades a great amount of educational research has focussed on the ideas which students have in relation to scientific concepts (see Driver, 1989). It is now well established that during their experiences in everyday life children develop their own "naive theories" which they use to explain the natural phenomena which they observe in the world around them. The existence of these ideas amongst students has been demonstrated in a wide range of sciences including physics (e.g., McCloskey, 1983), chemistry (e.g., Stavy, 1991), biology (see Wandersee & Mintzes, 1987), astronomy and earth science (e.g., Sadler, 1987; Vosniadou & Brewer, 1989).
Several different terms have been commonly used to describe these ideas. The various terminologies have included "misconceptions" (e.g., Doran, 1972; McClelland, 1985), "children's science" (Osborne & Freyberg, 1985) and "world knowledge" (Gunstone, Champagne & Klopfer, 1981). Other researchers have used terms such as "alternative frameworks" (Driver & Easley, 1978) which reflect the nature of the mental organisations involved. This problem of nomenclature has been discussed by Abimbola (1988) who has suggested that the term "alternative conceptions" should be generally adopted chiefly because it is more inclusive over different branches of science. For this reason the term "alternative conceptions" will be the one adopted in this study.
In her review of the literature on students' conceptions, Driver (1989) stated that (italics inserted) "One open question is the extent to which children's conceptions are genuinely 'theory-like', that is having a coherent internal structure and being used consistently in different contexts" (p.483). Studies by McCloskey (1983) on conceptions of motion and Vosniadou and Brewer (1989) on conceptions of the Earth's shape indicated that students did apply their conceptions in a theory-like way. However, other studies have suggested otherwise. Halloun and Hestenes (1985) surveyed university physics students and concluded that "nearly every student used some mixture of concepts .... and appeared to be inconsistent in applying the same concept in different situations [concerning linear and projectile motion]" (p. 1058). Similarly, Finegold and Gorsky (1991) presented university and high school students with questions concerning periodic, linear and projectile motion and found that students' conceptions were not consistently applied. Summers and Kruger (1992) found inconsistencies in their subjects' descriptions of energy, and Engel Clough and Driver (1986) reported that "students were using different alternative frameworks in response to parallel questions" (p. 489) on pressure, heat and inheritance. Thus, it appears that in many cases, students do not apply their conceptions in a way which a scientist would consider to be consistent.
The ability to generalise principles to a range of situations is generally considered to be important in science education. Thus it is important to understand the factors which affect the ability of students to generalise their conceptions even though these conceptions may be at odds with accepted scientific viewpoints. Engel Clough and Driver (1986) noted the importance of the context (or setting) of the question in determining an individual's response. Some authors have successfully identified critical contexts which influence students' conceptions. For example, Chi, Feltovich and Glaser (1981) found that novices tended to classify mechanics problems according to the types of physical objects which were in the questions. Whitelock (1991) and Fischbein, Stavy and Ma-Naim (1989) studied students' conceptions of motion and found that the type of moving body was an important factor for some. It thus appears that in many cases the context of the question plays a significant role in determining how a student will respond.
This factor therefore should be of critical importance when diagnosing specific alternative conceptions in target populations. For example, it is conceivable that a student could answer one particular question regarding motion in such a way as to indicate the presence of an alternative conception, but if the question was rephrased into a different context the student could respond completely differently. As a result the response of a student to one particular question may be very context-specific and may not give a reliable indication of that student's conceptions of the topic in a broader sense. This could be referred to as a "contextual error" in the diagnosis. However, it is sometimes necessary to survey students' conceptions in a broad range of topics in a single study, and in these cases, diagnoses have been determined on the basis of responses to a single question only (e.g., Helm 1980; Schoon 1989; Taiwo, 1976). In studies such as these, the responses of students are limited to one specific context and this could theoretically lead to a certain amount of error in the results because the students may respond differently to other contexts. With this problem in mind, the aim of the present study is to answer the following question:
In what proportion of Year 10 students does contextual error occur in the diagnosis of a specific alternative conception?For the purposes of this study, contextual error will be defined as those responses which are misleading because they do not give an accurate guide to the students' conceptions of the topic in a broader sense.
Methodology
The choice of context
The alternative conception which has probably received the most intensive study is the idea that a continuous action of a force is necessary to keep an object in motion (Osborne 1981; McCloskey, 1983; Viennot, 1979). Although it represents a way of thinking which has been long rejected by the scientific community it has now been established that this idea predominates amongst both secondary students (Sadanand & Kess, 1990; Watts & Zylbersztajn, 1981) and tertiary students (Clement, 1982). For the purposes of this study the alternative conception is stated as being that "if an object is in motion then the main force on it is in the same direction as the motion".
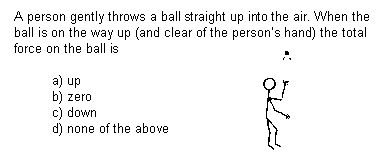
In research studies, this particular alternative conception is often identified in target populations by using an item concerning a ball being tossed vertically (e.g., Gunstone, 1990; Osborne, 1981; Smith & Peacock, 1992; Thijs 1992). It was therefore decided that the context of a ball rising vertically would form a suitable specific context for comparison with a broader range of contexts involving linear motion. On this basis, Question 1 (in which the context is very similar to a question described by Osborne (1981) was included in the instrument (see Figure 1).

Figure 1: The item concerning a ball being tossed vertically (Question 1)
The instrument
It was decided to use multiple choice questions as these are often used to identify people who hold certain alternative conceptions. Wandersee and Mintzes (1987) found that multiple choice tests were the second most common research method (after interviews) used in studies of students' conceptual development in the life sciences, and they have often been used to diagnose students' alternative conceptions with respect to forces and motion (e.g., Brown & Clement, 1987; Licht & Thijs, 1990; Whitaker, 1983). The accepted practice in studies such as these is to use an identified alternative conception as a distracter in the multiple choice question.
The instrument consisted of a test entitled "Forces in Sport" containing 10 multiple choice questions. Two of the 10 were distracter questions, not related to the investigation (- these were included to break up the test and reduce the possibility of students answering in a pattern). The 8 test questions (comprising Question 1 and 7 others) were all of a similar level of difficulty and concerned the direction of the main or total force on a freely moving object in linear motion. They were written in simple language, described daily-life situations, and each was accompanied by a simple, line drawing to illustrate the problem. Each question had a scientifically correct response, one distracter which indicated that "motion implies force", and two other plausible distracters. The eight test questions are reproduced in the Appendix.
The context of the questions was systematically varied along three parameters : the nature of the moving object, the direction of the motion and the rate of the motion. Question 1 concerned a ball being thrown gently in a vertical direction, the second question concerned a cyclist moving quickly in a horizontal direction, the third question concerned a golf ball moving gently in a horizontal direction, the fourth question concerned a trampolinist moving quickly in an upwards direction, the fifth question concerned a girl on roller skates moving slowly in a horizontal direction, the sixth question concerned a cricket ball moving rapidly in a vertical direction, the seventh question concerned a hockey ball moving quickly in a horizontal direction, and the eighth question concerned a "winning coach" being gently tossed vertically upwards. In half the questions the moving object was a ball and in the other half the moving object was a person; in half the questions the direction of motion was vertical and in the other half it was horizontal; and in half the questions the implied rate of motion was "gentle" while in the other half it was "quick".
The questions were similar in that each one could be correctly answered by reasoning that because the object was slowing down therefore the main force must have been operating in the opposite direction to the motion. Conversely, the "motion implies force" distracter in each question would be chosen by students who reasoned that because the object was moving forward then the main force must be in the same direction as the motion.
As suggested by Tamir (1990) subjects were asked to choose the best answer, rather than the correct answer. This had the advantage of requiring the students to analyse the relative importance of the options, if they believed that more than one was correct.
The test was validated by three physics lecturers. Its reliability, based on the group described below, was shown to be acceptable (Cronbach's alpha = 0.81 for the correct response; and Cronbach's alpha = 0.79 for the "motion implies force" distracter). Each of the questions had an acceptable difficulty index (ranging from .39 to .61), discrimination index (ranging from .19 to .26) and distracter efficiency (ranging from .01 to .16).
Sampling procedure
The test was administered to 567 Year 10 students (15-16 year olds) in four secondary schools in a regional city in south eastern Australia. The schools were located in different parts of the city and represented a variety of educational practices: co-educational and single sex schools (of both types) with classes either streamed or unstreamed. All the students had studied forces at high school although some more recently than others.
The students were asked to answer every question on the test, and were given enough time to do this (usually about 10-15 minutes) under test conditions. Because the analysis of data required the assumption that 8 questions had been answered, twenty two students who did not answer every question were not included in the analysis.
Results
Raw results
In each question, both the correct answer and the "motion implies force" distracter attracted more responses than the other two distracters. The students were grouped according to how frequently they chose the "motion implies force" distracter over the eight test questions and the results are presented in Figure 2.
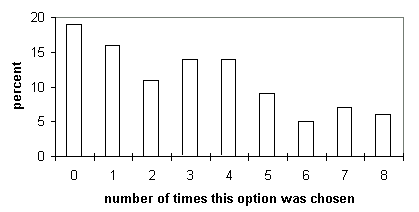
Figure 2: How often students chose the "motion implies force" distracter
Figure 2 shows that the majority of the students did not answer the questions consistently. Of the 545 students, 81% chose the "motion implies force" distracter at least once, but the average number of times that this distracter was chosen was 3.1 out of the possible 8. Only 6% (N=34) of the students were totally consistent, choosing this distracter for all 8 questions. It thus appears that the majority of the students were not treating all the questions in the same way, and were choosing the "motion implies force" distracter in some questions but not others.
Analysis of error
The first step in the analysis was to set an arbitrary level of responses which could be used to identify those students who answered the questions in a reasonably consistent (but not necessarily totally consistent) way. These students would presumably be the ones who had a fairly strong belief that "motion implies force" in situations involving linear motion. This "target group" would be the students whom a researcher would presumably most want to identify when investigating this alternative conception.
It was decided that any student who chose the distracter indicating that "motion implies force" on 5 or more occasions for the 8 questions would belong in this category. There were two reasons for this:
A similar analysis was carried out for each of the other 7 questions in the instrument. The combined results are presented in Figure 3. This shows that although the actual proportions varied slightly the other questions had a similar level of error to Question 1. We can therefore conclude that this result is not an artefact of one particular context.
Lastly, the level of error in Question 1 was also determined with regard to the scientifically correct answer. It was found to be 20% - a level which is comparable to that of the "motion implies force" distracter. This implies that contextual error also occurs with respect to the scientifically correct responses.

Figure 3: Proportion of error calculated for each question
Discussion
Although many of the students in this study selected the "motion implies force" distracter in some questions, very few consistently chose it in the full range of everyday situations which were presented. It thus appears that many of these students were not responding to the questions in a way in which a scientist would consider to be consistent. To this extent, the results support the findings of other researchers who have suggested that students' conceptions are not applied consistently (Finegold & Gorsky, 1991; Halloun & Hestenes, 1985). Some researchers have studied the reasons for this lack of consistency. Reif (1987) concluded that "novice students' knowledge about a scientific concept is highly fragmented and does not specify how to interpret a concept in specific instances" (p. 318). In order to solve a problem involving physical phenomena physics students would "rely on various special knowledge elements stored in memory, try to retrieve one of these, and apply it without much subsequent reasoning" (p. 316) rather than referring to general laws or concepts. Other studies have noted the effect of context on students' responses. For example, Chi et al. (1981) found that novices were influenced by the types of physical objects, such as "rotational things" or "blocks on inclined planes" when attempting to classify problems in mechanics. Further support for this has been provided by Fischbein et al. (1989) who found that amongst tenth and eleventh grade students the action of impetus depended on the features of the moving body and in particular its shape, weight and function. Similarly, Whitelock (1991) tested students aged 7-16 and found that "the animate nature of moving objects....was an important distinction in subjects' consideration of causes of motion" (p. 321). It is therefore possible that in the present study, the observed lack of scientific consistency can be largely attributed to the variations in context.
An inescapable result of lack of consistency in a particular topic is that if a student answers the majority of the questions in one way and a minority of the questions in another way then there is a chance that if a researcher uses a "minority" question as a diagnostic item then it could give a misleading indication of that student's conceptions over the topic as a whole. In the present study, these erroneous responses accounted for just under 17% of the total. It was also evident that within the limits of this study it was not possible to identify a particular context which did not result in a similar level of error.
This suggests that contextual error is a factor affecting the diagnostic accuracy of individual items. The "inaccurate" results in this study may in fact accurately reflect students' responses to particular contexts but they are misleading (or erroneous) because they do not give any indication of the way in which students would presumably answer most questions about linear motion. The main implications of this are that presumably, the results of studies which use only one diagnostic question per topic may be to some extent context specific and that accuracy of diagnosis would be improved by the use of additional questions on the same topic but covering a range of different critical contexts (e.g., varying the features of the moving body).
However, the results of this study are not necessarily applicable to all cohorts of students. For example, it is possible that contextual error would be lower amongst older students than younger ones - Licht and Thijs (1990) investigated alternative conceptions associated with Newton's Third Law and found that pupils in higher grades were more consistent than those in lower grades. There is some evidence that this trend also applies to "motion force" conceptions - Halloun and Hestenes (1985) found that 40% of their university students were completely consistent, compared with only 6% of the 15-16 year olds in the present study. If younger students are less consistent then it might be expected that the diagnostic accuracy of an individual question would be less for these lower age groups. It is therefore possible that a greater number of items is required for accurate diagnosis in student groups, such as the one in the present study, in which consistency is low.
In conclusion, the present study has indicated that contextual error does occur and that it was a factor which resulted in inaccurate diagnoses of alternative conceptions in about 17% of the students. One might be tempted therefore to suggest that a similar level of error might exist in studies which have used single items to identify alternative conceptions in specific topics, so their results should be interpreted accordingly. However, this sort of claim would be premature until topics other than linear motion have been investigated in this way, and until the critical contexts in these topics have been identified. This clearly represents an extensive and potentially rewarding avenue for future research.
Acknowledgments
I am grateful to Jim Miles for his advice during the preparation of this manuscript.
References
Abimbola, I. O. (1988). The problem of terminology in the study of student conceptions in science. Science Education, 72(2), 175-184.
Brown, D.E., & Clement, J. (1987). Misconceptions concerning Newton's Law of Action and Reaction: The underestimated importance of the Third Law. In J. Novak (Ed.) Proceedings of the Second International Seminar on Misconceptions and Educational Strategies in Science and Mathematics, Vol. 3, (pp. 38-55). Ithaca, Cornell University.
Chi, M., Feltovich, P., & Glaser, R. (1981). Categorisation and representation of physics problems by experts and novices. Cognitive Science, 5, 121-152.
Clement, J. (1982). Students' preconceptions in introductory mechanics. American Journal of Physics, 50(1), 66-71.
Doran, R. L. (1972). Misconceptions of selected science concepts held by elementary school students. Journal of Research in Science Teaching, 9(2), 127-137.
Driver, R. (1989). Students' conceptions and the learning of science. International Journal of Science Education, 11(5), 481-490.
Driver, R., & Easley, J. (1978). Pupils and paradigms: A review of literature related to concept development in adolescent science students. Studies in Science Education, 5, 61-84.
Engel Clough, E., & Driver, R. (1986). A study of consistency in the use of students' conceptual frameworks across different task contexts. Science Education, 70(4), 473-496.
Finegold, M., & Gorsky, P. (1991). Students' concepts of force as applied to related physical systems: A search for consistency. International Journal of Science Education, 13, 97-113.
Fischbein, E., Stavy, R., & Ma-Naim, H. (1989). The psychological structure of naive impetus conceptions. International Journal of Science Education, 11(1), 71-81.
Gunstone, R. F. (1990). "Childrens' science": A decade of developments in constructivist views of science teaching and learning. Australian Science Teachers Journal, 36(4), 9-19.
Gunstone, R. F., Champagne, A. B., & Klopfer, L. E. (1981). Instruction for understanding: A case study. Australian Science Teachers Journal, 27(3), 27-32.
Halloun, I., & Hestenes, D. (1985). Common sense concepts about motion. American Journal of Physics, 53, 1056-1065.
Helm, H. (1980). Misconceptions in physics amongst South African students. Physics Education, 15, 92-97.
Licht, P., & Thijs, G. (1990). Method to trace coherence and persistence of preconceptions. International Journal of Science Education, 12, 403-416.
McClelland, J. A. G. (1985). Misconceptions in mechanics and how to avoid them. Physics Education, 20, 159-162.
McCloskey, M. (1983). Intuitive physics. Scientific American, 248(4), 114-122.
Miles, J., lecturer in statistics, personal communication.
Osborne, R. (1981). Science education: Where do we start? Australian Science Teachers Journal, 28(1), 21-30.
Osborne, R., & Freyberg, P. (1985). Learning in science: The implications of children's science. Auckland: Heinemann.
Reif, F. (1987). Instructional design, cognition and technology: Applications to the teaching of scientific concepts. Journal of Research in Science Teaching, 24(4), 309-324.
Sadanand, N., & Kess, J. (1990). Concepts in force and motion. The Physics Teacher 28(8), 530-533.
Sadler, P. M. (1987). Misconceptions in astronomy. In J. Novak (ed) Proceedings of the Second International Seminar on Misconceptions and Educational Strategies in Science and Mathematics, Vol. 3, (pp. 422-425). Ithaca, Cornell University.
Schoon, K. J. (1989). Misconceptions in the Earth sciences: A cross-age study. Paper presented at the 62nd annual meeting of the National Association for Research in Science Teaching, San Francisco, California.
Smith, R. G., & Peacock, G. (1992). Tackling contradictions in teachers' understanding of gravity and air resistance. Evaluation and Research in Education, 6(2&3), 113-127.
Stavy, R. (1991). Children's ideas about matter. School Science and Mathematics, 91(6), 240-244.
Summers, M., & Kruger, C. (1992). Research into English primary school teachers' understanding of the concept energy. Evaluation and Research in Education, 6(2&3), 95-111.
Taiwo, D. (1976). A study of the nature of incidental physical science knowledge possessed by elementary school children in Western State of Nigeria. Journal of Research in Science Teaching, 13(6), 565-568.
Tamir, P. (1990). Justifying the selection of answers in multiple choice items. International Journal of Science Education, 12, 563-573.
Thijs, G. D. (1992). Evaluation of an introductory course on "force" considering students' preconceptions. Science Education, 76(2), 155-174.
Viennot, L. (1979). Spontaneous reasoning in elementary dynamics. European Journal of Science Education, 1(2), 205-221.
Vosniadou, S., & Brewer, W. F. (1989). The concept of the Earth's shape: A study of conceptual change in childhood. Manuscript (University of Illinois, Illinois).
Wandersee, J. H., & Mintzes, J. J. (1987). Childrens' biology: A content analysis of conceptual development in the life sciences. In J. Novak (Ed.) Proceedings of the Second International Seminar on Misconceptions and Educational Strategies in Science and Mathematics, Vol. 2, (pp. 522-534). Ithaca, Cornell University.
Watts, D. M., & Zylbersztajn, A. (1981). A survey of some children's ideas about force. Physics Education, 16, 360-365.
Whitaker, R. J. (1983). An examination of student inconsistencies in their understanding of trajectory motion. In H. Helm and J. Novak (Eds) Proceedings of the International Seminar: Misconceptions in Science and Mathematics (pp. 420-425). Ithaca, Cornell University.
Whitelock, D. (1991). Investigating a model of commonsense thinking about causes of motion with 7 to 16-year-old pupils. International Journal of Science Education, 13, 321-240.
| Please cite as: Palmer, D.H. (1998). Measuring contextual error in the diagnosis of alternative conceptions in science. Issues in Educational Research, 8(1), 65-76. http://www.iier.org.au/iier8/palmer.html |
© 1998 Issues in Educational Research
Last revision: 9 Oct 2013. This URL: http://www.iier.org.au/iier8/palmer.html
Previous URL: http://education.curtin.edu.au/iier/iier8/palmer.html
Previous URL from 1 Mar 1999 to 1 Aug 2001: http://cleo.murdoch.edu.edu.au/gen/iier/iier8/palmer.html
HTML: Clare McBeath [c.mcbeath@bigpond.com] and Roger Atkinson [rjatkinson@bigpond.com]