Issues In Educational Research, Vol 13, 2003
[ Contents Vol 13 ] [ IIER Home ]

Does the playing of chess lead to improved scholastic achievement?

Murray Thompson
Flinders University

The effect of playing chess on problem solving was explored using Rasch scaling and hierarchical linear modelling. Subjects were 508 students from Grades 6 - 12 in an Australian Independent boys school, with a strong tradition in the game of chess. Of these 508 students, 64 were regular players of competitive chess. Data from the Australian Schools Science Competition were Rasch scaled and placed on a single scale for all the grades. Multilevel analysis using hierarchical linear modelling was employed to test the effects of the hypothesised variables. No significant effect of the playing of chess on the scholastic performance was found, suggesting that previous results showing positive effects may have been due to other factors such as general intelligence or normal development. It is suggested that this combination of Rasch scaling and multilevel analysis is a powerful tool for exploring such areas where the research design has proven difficult in the past.

Introduction

The game of chess has long been associated with strategic thinking and problem solving. De Groot (1965, 1966) explored the difference between expert and novice chess players. Experts and novices were shown chess boards with pieces in position from an actual game for a period of five seconds. Experts were able to recall the positions of 20 or more pieces, while novices were only able to recall four or five. On the other hand, when presented with pieces placed randomly on the board and not from a game, the experts performed no better than the novices. Chase and Simon (1973) have suggested that the experts are able to chunk the information into meaningful patterns related to the game. More recently, in the literature concerned with expert performance, chess is often used as a target domain (Ericsson et al 1990, Ericsson, 1996, Charness et al 1996, Ericsson & Lehmann 1996). This is partly due to the interval scale of performance which is afforded by the international rating scale devised by Elo (1986). This has allowed the use of such statistical techniques as regression analysis to explore the factors associated with expert performance. The consistent finding in this literature on expert performance is that expertise in chess depends upon deliberate practice and serious study of the game (Ericsson et al 1990, Ericsson 1996, Charness et al 1996, Ericsson & Lehmann 1996). One particular suggestion (Charness et al 1996) is that, contrary to popular belief, there is a lack of evidence for the view that innate talent is important in the development of chess expertise. Indeed it is suggested that what has been regarded as talent, may well be a product of motivation and practice.

Chess enthusiasts have long argued that the playing of chess leads to improved scholastic attainment and greater self-confidence. It is suggested that the playing of chess develops skills of creative thinking, critical thinking and the ability to concentrate and to solve problems. Certainly, there is no doubt that playing competitive chess demands considerable concentration skills. Even at the junior chess level, games are often as long as three hours. Playing chess also demands an ability to project possible positions of pieces and so could help develop visual and spatial abilities. Similarly, chess demands skills of logical thinking. It might be argued that these sorts of skills and abilities should transfer to other scholastic areas. The famous chess master Kasparov has promoted chess in schools and a number of programs have emerged which have been fostered by the various chess associations, particularly in the United States. In an interview reported by Harrell (1999), LaFreniere, the Coordinator of the Washington Chess Federation Scholastic Chess Program said,

Chess is the single most powerful educational tool we have at the moment, and many school administrators are realising that. (Harrell, 1999 on net)

Although not always widely published beyond chess circles, there have many research projects on the effects of chess on student performance in the classroom. Frank (1974) explored the relationship between playing chess and other scholastic abilities. He found that there was a significant correlation between chess playing and spatial and numerical abilities and that there was a positive correlation between playing chess and the change in numerical and verbal aptitudes. Christiaen (1976) randomly divided 40 fifth grade students into experimental and control groups. The students were given a number of tests of cognitive development at the end of their fifth grade studies and again at the end of their sixth grade studies. The experimental group received 42 one-hour chess lessons. The tests at the end of both the fifth and the sixth grade showed significant differences in favour of the chess group.

Ferguson (1983) studied the effects of chess treatment and computer treatment on groups of academically gifted students in Grades 7 to 9. The chess treatment group showed a significant difference in the growth of originality. Horgan (1987) advocated the teaching of chess as a means of developing a child's intellect. Ferguson (1987) showed that a group of sixth grade students who had not previously played chess, showed significant development in memory and reasoning skills when they played chess daily over a period of nine months. Margulies (1991) found that elementary pupils, who played chess, showed a significant improvement in reading ability when compared to their non-chess playing fellows. Gaudreau (1992) has reported that in a group of fifth grade students, those who had their mathematics instruction enriched with chess, developed significantly better problem solving abilities than those who had received a normal mathematics program. Much of this material has been summarised by Dauvergne (2000).

In summary, it is argued that chess can be an intrinsically motivating learning tool. Performance at chess cannot be blamed on anyone else and students must accept the consequences of their actions. They must develop skills of planning, of problem solving, evaluating a wide range of alternatives, concentration, and self-discipline. It is clear that the devotees of the game of chess are convinced of its worth as a powerful educational tool. They argue that it is a simple and cheap means of helping students to develop important cognitive skills.

Some research problems

The studies reported and discussed above are to be found predominantly on various web-pages, in the chess literature and in the teachers' journals rather than in the literature of cognitive psychology. However, there has been a continuing interest in chess in cognitive psychology, but not its effect on scholastic achievement. Perhaps this reflects the quasi-experimental nature of much of the research or perhaps it is a result of the view that those who play chess are the smart students who would have performed equally well without chess. The learning and the playing of chess take a considerable period of time and practice and any improvement in scores in cognitive tests may be confused with the normal development of the students. Thus the usual experimental design for investigating the effects of an instructional intervention has an experimental group and a control group and utilises a pre-test and post-test arrangement, which compares one group with the other. In school situations, such designs can be very difficult to maintain effectively, with so many other intervening factors. For example, the two groups will often be two intact class groups and so the "random assignment of students" to the groups is in reality a random assignment of treatments to the groups. Moreover, as intact groups, it is likely that their treatments may differ in a number of other ways. For example, they may have different teachers, or the very grouping of the students themselves may have an effect. In addition, there is the risk that any positive effect may be due to a Hawthorne effect rather than the treatment itself.

It seems that the traditional pre-test and post-test experimental designs have led to results which while encouraging, have not been conclusive and need further support. The difficulties in experimental design make it desirable to use statistical control, employing regression analysis procedures, to take into account the effects of other factors.

A study into the scholastic effects of chess

It has been suggested then that the learning and playing of chess helps students to develop a range of cognitive skills. (Harrell, 1999 on net). These skills include planning, problem solving, evaluating a wide range of alternatives, concentration, and self-discipline. If this is the case, then students who play chess ought to perform better at those scholastic tasks that involve these skills.

This study seeks to investigate whether there is any effect associated with chess playing in a group of students for whom some data are readily available. This study seeks to avoid the problems mentioned above by the use of statistical control in order to distil out the effects of the other factors. It does this by using data from the Australian Schools Science Competition which is Rasch scaled and then uses hierarchical linear modelling to explain this data in terms of the other variables, including the playing of chess.

The Australian schools science competition

The Australian Schools Science Competition is an Australia wide competition that is held every year. Students in Grades 3 - 12 compete in this multiple-choice test. The competition is administered by the Educational Testing Centre of the University of New South Wales. Faulkner (1991) outlined the aims of the competition and gave a list of items from previous competitions. Among its aims are the promotion of interest in science and awareness of the relevance of science and related areas to the lives of the students, and the recognition and encouragement of excellence in science. An emphasis is placed on the ability of students to apply the processes and skills of science. Since the science syllabi throughout Australia vary, the questions that are asked are essentially independent of any particular syllabus and are designed to test scientific thinking. Thus, the questions are not designed to test knowledge, but rather to test the ability of the candidates to interpret and examine information in scientific and related areas. Thus students may be required to analyse, to measure, to read tables, to interpret graphs, to draw conclusions, to predict, to calculate and to make inferences from the data given in each of the questions. It seems logical then that involvement in chess should confer an advantage to individual students in the Australian Schools Science Competition.

It is hypothesised then that students who play chess regularly should perform better in the Australian Schools Science Competition than those who do not, when controlling for the other variables that may be involved.

Rasch scaling and item response theory

The Rasch model of test scaling has come into prominence over recent times and it has become the basis of many testing programs throughout the world. Snyder and Sheehan (1992) provide a good introduction to the principles of Rasch scaling. The power of the Rasch scaling method is that the measurement of the performance of the students taking the test is independent of the test items and that the difficulty of the test items is independent of the group of students used to calibrate them. Essentially, this model assumes that the likelihood of a student correctly answering a question will depend upon the difference between the difficulty of the item and the performance level of the student, both measured along a continuum, known as the latent trait continuum.

A number of computer programs have been developed to assist with the analysis of data from test items. One of these is the QUEST program (Adams and Siek-Toon Khoo 1993), which allows the results of tests to be analysed to determine whether they fit the Rasch model and provides estimates, both of the abilities of the students and the difficulties of the test items. In a recent study (Thompson 1998), it was found that the Australian Schools Science Competition data fit the Rasch model well, allowing the estimates of the item difficulties and the student abilities to be plotted on the same scale. The Rasch Scaling process allows the possibility of placing the tests at each of the grade levels on the same scale, thereby allowing direct comparisons between the grade levels. The study by Thompson (1998) showed that it is possible to put the results from the different grade levels on the same scale using concurrent equating, which provides good agreement with the expected results. This involves scoring all of the items and subjects at the one time, relying on the common items to establish the difficulty levels of all of the items across the range. This method was tested in comparison to other equating procedures by Mohandas(1998) and concurrent equating provided good agreement with the expected results. It is therefore possible to put the items and subjects from all the grade levels onto one scale.

Factors affecting performance in the science competition

The performance of an individual student in the Science Competition may be influenced by a number of factors. Since all of the students from Grades 6 -12 can be placed according to their performance on a single scale, clearly their grade level will be an important factor influencing their performance. Similarly, the basic ability of the student, as might be measured using a standardised IQ test, and the grouping of the students in their classes could reasonably be expected to have an effect on the individuals. As well, it is hypothesised that the playing of chess might be a factor that will have a measurable effect. Other factors that may affect the performance of the students are their individual involvement in other pursuits, such as music. In order to examine the relative effect of each of these factors it is necessary to use hierarchical linear modelling analysis.

These hierarchical linear models are discussed by Bryk and Raudenbush (1992), Raudenbush and Bryk (1997), and Keeves and Sellin (1997). Such models allow a researcher to postulate and subsequently to test statistical hypotheses associated with relationships between the outcome variable and the factors that may affect it. In hierarchical linear models, the researcher can examine the effect of the various factors, both within and between individuals and at the group level and any possible interactions between them. The outcome variable is represented as a function of the various characteristics. Thus in the example of the Science Competition, the outcome variable is the Rasch scaled score of the individual and the variables of IQ and chess playing can become level one variables in an hierarchical model.

First, there is the between student within the class group equation

Y_ij = _j0 + _j1(IQ) + _j2(chess) + r_ij (1)

In equation (1) Y_ij represents the performance of student i in group j and beta

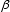_j0 represents the baseline performance. Each of the coefficients represents the extent to which the performance of a student is affected by the variable in the brackets. The coefficient beta

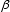_j1 represents the effect of student IQ and the variable is the measured IQ of the student, whilst beta

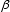_j2 represents the effect of playing chess and its associated variable is a dichotomous variable indicating whether the student plays chess or not. The term r_ij represents the random error. An important feature of hierarchical linear models is that these coefficients will vary from student to student.

At the second or macro level of a hierarchical linear model, the coefficients in the Level 1 equation are expressed as an outcome variable in a linear equation of Level 2 variables at the second or between class group level. For example, the coefficient 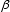beta _j1, the effect of IQ on the performance of student i, may be expressed as a function of grade level. Likewise, the intercept 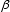beta _j0 may be expressed as a function of grade level and other treatment conditions.

Thus, a researcher may build a model as follows in equations (2) and (3), as a between class group equation

_j0 = ₀₀ + ₁₀(grade) + ₁₀(other treatment) + u_j0 (2)
_j1 = ₀₁ + ₁₁(grade) + ₁₁(other treatment) + u_j1 (3)

It can be seen then that a layered or hierarchical model is being employed. The values of the various coefficients need to be estimated using the data available from the Australian Schools Science Competition. Recent advances in computational technology make such estimations possible. One program which does this by an iterative method using empirical Bayes estimation procedures based on maximum likelihood estimates is HLM, developed by Raudenbush and Bryk (1996). With this facility, it is possible to estimate the effects of the various parameters and their inter-relationships at each of the levels of the hierarchical linear model.

It follows then, that it may be possible using a hierarchical linear model, to partition out the effects of the variables such as IQ, together with the effect of playing chess, which is of interest in this study, and to estimate the effect of each of these variables on student performance.

Research question

Does regular involvement in competitive chess relate to a positive effect on student performance in the Australian Schools Science Competition? If, as is hypothesised, the regular playing of chess is a significant factor in the performance of the students, then it ought to be possible to measure this effect and to test its statistical significance and compare it to other factors, such as normal yearly development or learning.

Research methods

This study uses data from an independent boys school with a strong tradition of chess playing. The school fields teams in competitions at both the primary and secondary levels and so a significant and identifiable group of the students plays competitive chess in the organised inter-school competition and practise chess regularly. Each of these students played a regular fortnightly competition and was expected to attend weekly practice, where they received chess tuition from experienced chess coaches. The students had also taken part in the Australian Schools Science Competition as part of intact groups and data from 1999 for Grades 6 - 12 were available for analysis. IQ data were readily available for the students in Grades 6 -12. Subjects, then, were all boys (n= 508) in Grades 6 -12, for whom IQ data were available. Of these 508 students 64 were competitive chess players. Rasch scaling, with concurrent equating, was used to put all of the scores on a single scale. These scores were then used as the outcome variable to be explained using a hierarchical linear model, and the variables of IQ, chess playing, other class level factors, grouping and grade to see if the playing of chess had a significant effect on the performance of the students. A dichotomous variable was used to indicate the playing of chess, with chess players being given 1 and non-players 0. Chess players were defined as those who represented the school in competitions on a regular basis.

Results

The individual responses for all of the subjects for the 249 different items of the science competition data were analysed using the QUEST program (Adams and Siek-Toon Khoo 1993). These items were arranged in such a way as to allow for concurrent equating of items common to more than one of the grade level tests. It was found that of the 249 items, only eight did not fit the Rasch model with their infit mean square values being outside the acceptable range. These items were deleted from the analysis and the program was run once again. The use of concurrent equating allowed the performance ability of each subject to be placed on a single scale regardless of the grade level. The performance ability scores were then used as the outcome variable in a hierarchical linear model to be explained by the various parameters involved.

The initial model that was explored was as follows in equation (4).

Y_ij = _j0 + _j1(IQ) + _j2(chess) + r_ij (4)

In this Level 1 model, the outcome variable (the Rasch scaled performance ability score) is expressed as a function of IQ, and playing chess. At Level 2, the model sought to explain the coefficients at Level 1 in terms of factors associated with the grouping of the subjects as shown in equations (5) and (6).

_j0 = ₀₀ + ₁₀(grade) + ₁₀(other treatment) + u_j0 (5)
_j1 = ₀₁ + ₁₁(grade) + ₁₁(other treatment) + u_j1 (6)
and so on.

In each case, the other treatment was exploring whether the grouping of the students in their classes had any effect on the outcome.

This model was improved by the elimination of variables that did not prove to have a significant effect. The final model was as follows in equations (7), (8), (9) and (10). Level-1 model

Y = B₀ + B₁*(IQ) + B₂*(CHESS) + R (7)

In this Level 1 model, the outcome variable Y, the Rasch scaled performance scores measured by the Science Competition test are equal to an intercept or base level B0, plus a term that expresses the effect of IQ, with its associated slope, B1, and a term which expresses the effect of playing chess and its associated slope B2. There is also an error term R. Thus the outcome variable Y is explained in terms of IQ and involvement in chess at Level 1.

In the Level 2 model, the effect of the Level 2 variables on each of the B terms in the Level 1 model is given in equations (8), (9) and (10). Level-2 Model

B₀   =   G₀₀   +   G₀₁*(GRADE) + U₀      (8)
B₁   =   G₁₀   +   U₁      (9)
B₂   =   G₂₀   +   U₂      (10)

Thus in equation (8), the constant term B₀ is expressed as a function of Grade, with an associated slope G₀₁. Values of each of these terms are estimated and the level of statistical significance evaluated to assess the effect of each of the terms.

Initially, the HLM program makes estimates of the various values of the slopes and intercepts, using a least squares regression procedure and then using an iterative process improves the estimation using a maximum likelihood estimation and the empirical Bayes procedure. Table 1 shows the reliability estimates of the Level 1 data.

Table 1: Reliability estimates of the Level 1 data

Random Level-1 coefficient Reliability estimate

INTRCPT1, B₀ 0.664

IQ, B₁ 0.324

CHESS, B₂ 0.019

Table 2 shows the least -squares regression estimates of the fixed effects.

Table 2: The least -squares regression estimates of the fixed effects

Fixed Effect Coefficient Standard
Error T-ratio Approx degrees
of freedom P-value

For INTRCPT1, B₀ INTRCPT2, G₀₀ -1.645 0.178 -9.221 504 0.000

GRADE, G₀₁ 0.217 0.200 11.034 504 0.000

For IQ slope, B₁ INTRCPT2, G₁₀ 0.040 0.002 19.089 504 0.000

For CHESS slope, B₂ INTRCPT2, G₂₀ 0.120 0.091 1.323 504 0.186

Table 3 shows the final estimations of the fixed effects.

Table 3: The final estimations of the fixed effects

Fixed Effect Coefficient Standard
Error T-ratio Approx degrees
of freedom P-value

For INTRCPT1, B₀ INTRCPT2, G₀₀ -1.572 0.327 -4.81 20 0.000

GRADE, G₀₁ 0.208 0.057 5.69 20 0.000

For IQ slope, B₁ INTRCPT2, G₁₀ 0.036 0.003 13.67 21 0.000

For CHESS slope, B₂ INTRCPT2, G₂₀ 0.056 0.091 0.619 21 0.542

Table 4 shows the final estimation of the variance components.

Table 4: Final estimation of variance components

Random Effect Standard
Deviation Variance
Component df Chi-square P-value

INTRCPT1, U₀ 0.222 0.049 15 52.09 0.000

IQ slope, U₁ 0.007 0.000 16 29.84 0.019

CHESS slope, U₂ 0.053 0.003 16 20.48 0.199

Level-1, R 0.606 0.367

In order to calculate the amount of variance explained by the model, a null model, with no predictor variables was formulated. The estimates of the variance components for the null model are shown in Table 5.

Table 5: Estimated variance components for the null model

Random Effect Standard
Deviation Variance
Component df Chi-square P-value

INTRCPT1, U₀ 0.602 0.362 21 357.7 0.000

Level-1, R 0.749 0.561

Using the data from Tables 4 and 5, the amount of variance explained is calculated as follows:

Variance explained at Level 2   =   0.362 - 0.049
0.362   =   0.865

Variance explained at Level 1   =   0.561 - 0.367
0.561   =   0.346

In addition, the intraclass correlation can be calculated.

rho   =   tau ₀₀
-----------
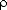tau ₀₀ + sigma ²   =   0.362
-----------------
0.362 + 0.561   =   0.392
----------------
0.362 + 0.561

This intraclass correlation represents the variance within groups compared to the total variance between and within groups. Thus the model is explaining 33.9 per cent (0.392 x 0.865) of the variance in terms of grade levels. The remaining 21.0 per cent ((1 - 0.392) x 0.346) is explained as the variation brought about by IQ and the playing of chess. In all 54.9 per cent of the variance in scores is explained by the model and 45.1 per cent is unexplained.

Discussion and interpretation of the results

In order to interpret the results, Table 2 is examined. The term G₀₀ represents the baseline level, to which is added the effect of the grade level to determine the value of the intercept B₀. The value G₀₀ represents the effect of the grade level and since this is statistically significant, it can be concluded from this that the students improve by 0.21 of a logit over one grade level, taking into account the effect of IQ and playing chess. The next important value is the term G₁₀, which indicates the effect of IQ on the performance in the Science Competition. Clearly this has a significant effect and even though the value seems very small, being 0.036, it must be remembered that it involves a metric coefficient for a variable whose mean value is in excess of 100 and has a range of over 50 units.

Of particular interest in this study is the value G₂₀. This represents the effect of playing competitive chess on the performance abilities of the students. It suggests that, taking into account the effects of IQ and grade level, students who play chess competitively, are performing at a level of 0.056 of a logit better than others, when controlling for the other variables of grade and IQ. This is approximately equivalent to one quarter of a year's work. However this result was not found to be significant. One possible explanation of this lack of significance is that the playing of chess has contributed to the individual student IQ and so the benefits of playing chess have been absorbed into the IQ variable.

This study has examined a connection between the playing of chess and the cognitive skills involved in problem solving. The results have not shown a significant effect of the playing of chess on the scholastic achievement of the students, when controlling for IQ and grade level.

Conclusion

The purpose of this study is to explore the relationship between the playing of chess and improved scholastic achievement. The difficulty in the research design associated with the intact groups of students has been overcome using the combination of Rasch scaling to place scores on a single scale and statistical control using a hierarchical linear model to obtain an estimate of the effect of playing chess and its statistical significance. The results of this study do not provide support for the hypothesis that the playing of chess leads to improved scholastic achievement. It is possible that the methodology of controlling for both grade level and IQ has removed the effect that has traditionally been attributed to chess, suggesting that those students who have been interested in chess have tended to be the more capable students. That is, the students who performed more ably at a particular grade level tended to have a higher IQ and there did not seem to be any significant effect of the playing of chess. This study provides a very useful application of both Rasch scaling and HLM and this method of analysis could be repeated easily in other situations.

References

Adams, R. J. & Khoo, Siek-Toon (1993). QUEST the interactive test analysis system. Hawthorn Vic: ACER.

Bryk, A. S. & Raudenbush, S. W. (1992). Hierarchical linear models: Applications and data analysis methods. Beverly Hills, Ca: Sage.

Bryk, A. S., Raudenbush, S. W., & Congdon, R. T. (1996). HLM for Windows version 4.01.01. Chicago: Scientific Software.

Charness, N., Kampe, R. & Mayr, U. (1996). The role of practice and coaching in entrepreneurial skill domains: An international comparison of life-span chess skill acquisition. In K. A. Ericsson (ed), The road to excellence. The acquisition of expert performance in the arts and sciences, sports and games. Mahwah NJ: Erlbaum.

Chase, W. G. & Simon, H. A. (1973). The mind's eye in chess. In W. G. Chase (ed), Visual information processing. New York: Academic Press.

Christiaen, J. (1976). Chess and cognitive development. Unpublished paper available from U.S. Chess Federation http://www.uschess.org/scholastic/sc-research.html

de Groot, A. D. (1965). Thought and choice in chess. The Hague: Mouton.

de Groot, A. D. (1966). Perception and memory versus thought. In B. Kleinmuntz (ed), Problem-solving. New York: Wylie.

Dauvergne, P. (2000). The case for chess as a tool to develop our children's minds [viewed 26 July 2000, verified 6 Jan 2004]. http://www.auschess.org.au/articles/chessmind.htm

Ferguson, R. (1983). Developing critical and creative thinking through chess. Unpublished paper available from U.S. Chess Federation http://www.uschess.org/scholastic/sc-research.html

Ferguson, R. (1987). The development of reasoning and memory through chess Unpublished paper available from U.S. Chess Federation http://www.uschess.org/scholastic/sc-research.html

Frank, A. (1974). Chess and aptitudes Unpublished paper available from U.S. Chess Federation http://www.uschess.org/scholastic/sc-research.html

Elo, A. E. (1986). The rating of chess players, past and present (2nd ed.). New York: Arco.

Ericsson, K. A. (1996). The acquisition of expert performance. In K. A. Ericsson (ed), The road to excellence. The acquisition of expert performance in the arts and sciences, sports and games. Mahwah NJ: Erlbaum.

Ericsson, A., Tesch-Römer, C. & Krampe, R. (1990). The role of practice and motivation in the acquisition of expert-level performance in real life. In M. J. A. Howe (ed), Encouraging the development of exceptional skills and talents. Leicester: BPS.

Ericsson, K. A. & Lehmann, A. C. (1996). Expert and exceptional performance: evidence of maximal adaptation to task constraints. Annual Review of Psychology, 47, 273-305.

Faulkner, J. (ed) (1991). The Best of the Australian Schools Science Competition. Rozelle, NSW: Science Teachers' Association of New South Wales.

Gaudreau (1992). Étude comparative sur ls apprentissages en mathematics 5e anné Unpublished paper available from U.S. Chess Federation http://www.uschess.org/scholastic/sc-research.html

Harrell, D. C. (1999). Schools try a new gambit: Chess to boost young minds. In Seattle Post-Intelligencer, 31 May 1999. [verified 6 Jan 2004] http://www.seattlep-i.com/local/ches31.shtml

Horgan, D. (1987). Chess as a way to teach thinking. Unpublished paper available from U.S. Chess Federation http://www.uschess.org/scholastic/sc-research.html

Keeves, J. P.and Sellin, N. (1997). Multilevel analysis. In J. P. Keeves, (ed), Educational research, methodology and measurement (2nd ed.), Oxford: Pergamon, pp. 3978-3987.

Margulies, S. (1991). The effect of chess on reading scores. Unpublished paper available from U.S. Chess Federation http://www.uschess.org/scholastic/sc-research.html

Mohandas, R. (1998). Test equating, problems and solutions: Equating English test forms for Indonesian junior secondary school final examinations administered in 1994. Unpublished Masters Thesis, The Flinders University of South Australia.

Raudenbush, S.W. & Bryk, A. S. (1997). Hierarchical linear models. In J. P. Keeves, (ed), Educational research, methodology and measurement (2nd ed.), Oxford: Pergamon, pp. 2590-2596.

Raudenbush, S. W. & Bryk, A. S. (1996). HLM Hierarchical linear and nonlinear modeling with HLM/2L and HLM/3L programs. Chicago: Scientific Software.

Snyder, S. & Sheehan, R. (1992). Research methods. The Rasch measurement model: An introduction. Journal of Early Intervention, 16(1), 87-95.

Thompson, M. J. (1998). The Australian Schools Science Competition - A Rasch analysis of recent data. Unpublished paper, The Flinders University of South Australia.

Weiss, D. J. and Yoes, M. E. (1991). Item response theory. In Hambleton, R. K. & Zaal, J. N. (eds), Advances in educational and psychological testing. Boston: Kluwer, pp. 69-95.

Acknowledgments

I am indebted to Professor John Keeves for his continued support and his insight into the complex problems of educational research.

Author: Murray Thompson is a part-time Doctor of Education student at Flinders University. As well he is an experienced secondary school teacher of Physics, Science and Mathematics at Prince Alfred College in Adelaide where he has held a number of positions of responsibility, including pastoral care, curriculum leadership and professional development. His research interests have revolved around educational measurement and cognitive psychology. Email contact address: dtmt@senet.com.au

Please cite as: Thompson, M. (2003). Does the playing of chess lead to improved scholastic achievement? Issues In Educational Research, 13(2), 13-26. http://www.iier.org.au/iier13/thompson.html

[ Contents Vol 13 ] [ IIER Home ]
© 2003 Issues In Educational Research. This URL: http://www.iier.org.au/iier13/thompson.html
HTML: Clare McBeath, Faculty of Education, Curtin University of Technology, [c.mcbeath@bigpond.com] and Roger Atkinson [rjatkinson@bigpond.com]
Created 6 Jan 2003. Last revision: 25 May 2006.

Random Level-1 coefficient	Reliability estimate
INTRCPT1, B₀	0.664
IQ, B₁	0.324
CHESS, B₂	0.019

Fixed Effect		Coefficient	Standard Error	T-ratio	Approx degrees of freedom	P-value
For INTRCPT1, B₀	INTRCPT2, G₀₀	-1.645	0.178	-9.221	504	0.000
For INTRCPT1, B₀	GRADE, G₀₁	0.217	0.200	11.034	504	0.000
For IQ slope, B₁	INTRCPT2, G₁₀	0.040	0.002	19.089	504	0.000
For CHESS slope, B₂	INTRCPT2, G₂₀	0.120	0.091	1.323	504	0.186

Random Effect	Standard Deviation	Variance Component	df	Chi-square	P-value
INTRCPT1, U₀	0.222	0.049	15	52.09	0.000
IQ slope, U₁	0.007	0.000	16	29.84	0.019
CHESS slope, U₂	0.053	0.003	16	20.48	0.199
Level-1, R	0.606	0.367

Variance explained at Level 2	=	0.362 - 0.049 0.362	=	0.865
Variance explained at Level 1	=	0.561 - 0.367 0.561	=	0.346