
 |
The concept of self-efficacy is based on the triadic reciprocality model symbolising a relationship between: (a) personal factors i.e. cognition, emotion, and biological events (b) behaviour, and (c) environmental factors (Maddux, 1995). Cognition, emotion and behaviour are the domains of personality which form the basis of research in self-efficacy. Research has been extensive on the relationship between self-efficacy and performance attainment in academic settings. Self-report scales are most commonly used in the assessment of self-efficacy. The guidelines to construct scales to assess self-efficacy have been specified by Bandura (2001). These guidelines highlight the importance of developing self-report measures which are task specific, and take into consideration all three domains of self-efficacy and three levels within each domain. Suggestions to develop measures which are reliable and have content validity have been provided. The major aims of the present research were to assess diverse students' self-efficacy in mathematics, and to assess its relationship with achievement. Self efficacy is viewed as a multidimensional construct which shares a reciprocal relationship with various determinants. The major determinants considered in this study include: (a) motivation strategies, (b) cognitive and metacognitive strategies, (c) resource management, (d) self-regulated learning, (e) meeting others' expectations, and (f) self-assertiveness. This article reports the findings and discusses the implications for student achievement in a multicultural learning context.
Perceived self-efficacy has been defined as "a generative capability in which cognitive, social, emotional, and behavioral subskills must be organised and effectively orchestrated to serve innumerable purposes" (Bandura, 1997, p.37). Self-efficacy mediates between an individual's ability and purposive action. Perceived self-efficacy influences the course of action adopted, effort invested, endurance and resilience in the face of obstacles and failures, coping, and the level of accomplishments. Self efficacy is also a crucial mechanism in individual agency (Bandura, 2001b). Crucial to exercising agency are: (a) planning, (b) forethought, which includes outcome expectations (c) self-evaluation, (d) motivation, and (e) self-regulation. Personal agency also works in tandem with proxy agency and collective agency. Proxy agency is the way an individual tries to get a person or people to be agents to achieve desired goals. Collective agency refers to beliefs shared among members of cultural groups in the collective power to attain desired results. Self-efficacy is conceptualised in this research as a holistic multi-dimensional construct which impacts on cognition, emotion, behaviour and goal attainment, and shares a reciprocal relationship with determinants such as motivation, self-regulation, cognition, resource management, and self-assertiveness.
Self-efficacy functions as a motivational facilitator of both learning and performance. Pintrinch and Schunk (2002) state that self-efficacy is a crucial variable in learning and performance of social, cognitive, motor skills, strategies and behaviours. They state that learnt skills will be performed only when the individual is motivated to display them. Self-efficacy is a crucial variable in this motivation to perform, that is, there has to be self-belief about the appropriateness of the situation and the consequences being positive. Reviewing research on the role of self-efficacy in academic motivation, Zimmerman (1995) highlights the causal link between self-efficacy and motivation. He concludes that self-efficacy is related to both indices of motivation, that is, the rate of performance and the expenditure of energy.
Self-efficacy and self-regulation share a reciprocal relationship. Self-efficacy operates during all phases of self-regulation, that is, forethought, performance, and self-evaluation based on reflection (Schunk & Ertmer, 1994). "Self-regulation is important because a major function of education is the development of life-long learning skills" (Zimmerman, 2002, p.66). Skills include: (a) setting specific proximal goals, (b) adopting strategies to attain the goals, (c) monitoring progress, (d) restructuring context to suit the goal, (e) efficient use of time, (f) self-evaluation of methods, and (g) attribution.
Attribution and self-efficacy have a bi-directional causal relationship. Attributions affect appraisal of self-efficacy and perceived self-efficacy biases causal attributions (Bandura, 1990). Ames (1990) contends that self-efficacy is determined as one develops by: (a) self-evaluation of one's ability versus effort at a task, and (b) attribution of success or failure to ability or effort. She points out that "older children also develop a more differentiated view of effort and ability. While effort can increase the chance of success, ability sets the boundaries of what one's effort can achieve. Effort now becomes the 'double edged sword'. Trying hard and failing threatens one's self-concept of ability" (pp.412-413). Feedback is another variable which has been researched in the context of self-efficacy. Undertaking tasks for which one has high perceived self-efficacy and received informed feedback are factors crucial to enduring motivation on tasks (Bandura & Cervone, 1986). Their study found that goals enhanced effort when self-evaluation against standards was combined with performance feedback.
Culture influences the development of efficacy. Oettingen (1995) states that information becomes useful only when it is appraised and cognitively processed through selection, weighting, and integration into self-efficacy judgments, and culture plays an influential role in this regard. Culture specific determinants also impact on efficacy and performance attainment (Gibson, 1999; Bempechat & Drago-Sevenson, 1999; O'Brien, Martinez-Pons, & Kopala, 1999). Gibson (1999), researching group efficacy and group effectiveness across tasks and cultures, had as independent variables level of task certainty, level of task interdependence, and level of collectivism. Results showed collectivism and interdependence to be significantly related to group efficacy and group effectiveness, with group efficacy and group effectiveness positively correlated with groups high on interdependence, and not significantly correlated with groups low on interdependence. In a cross-cultural study on self-regulation strategies, self-efficacy and achievement, Chye, Walker and Smith (1997) report differences in students' choice of learning strategies based on the country in which they were located. Singaporean students in Singapore were found to make greater use of effort regulation strategies than Singaporean students who studied in Australia. However the former scored less in use of organisational strategies than their counterparts in Australia. The authors reported strategies used as a better predictor of academic grade than self-efficacy. Bandura states that "Although efficacy beliefs have generalised functional value, how they are developed and structured, the ways in which they are exercised, and the purposes to which they are put, vary cross culturally" (2002, p.273). While stressing the need for assessing self-efficacy from a socio-cultural perspective, he contends that efficacy beliefs operate in a similar manner irrespective of the nature of the society. It is the way they are developed, exercised and the purposes for which they are used that vary across cultures.
In the current study, culture is constructed as a contextualised, dynamic, and evolving construct for every individual, and much more diverse than dichotomous categorisation of individuals into individualistic or collectivistic cultures. This is to accord for the multicultural nature of New Zealand society, and the intra-ethnic and intra-individual diversity within the cultural groupings. In the present research, while no comparisons are drawn between cultural groups, the distinct cultural identities of participants are valued and acknowledged. As stated by Bandura (2002)
[A] selected cultural factor that yields a small difference in group averages is generalized to all individuals in the cultural grouping as though they all believed and behaved alike as dichotomously classified.... Human behaviour is socially situated, richly contextualized and conditionally expressed. (p.276)In New Zealand, there has been a demographic shift in population over the years, along with increasing ethnic diversity in schools. The ethnic composition of classrooms is changing rapidly, and it is predicted that by 2040 the majority of students in New Zealand primary schools will be Mäori and Pasifika (Alton-Lee, 2003a). There is also a heterogeneous mix within each of the major ethnic groupings which include Päkehä European, Mäori, Asian, and Pasifika. Acknowledging this trend, and in the light of the evidence of wide disparities in academic achievement across schools and ethnic groups in New Zealand (New Zealand Government, 2001b), many initiatives have been furthered to raise achievement, reduce disparities, and close the gaps in education achievement among diverse groups (New Zealand Government, 2001a).
An area where some students lag behind is mathematics, and their "past experiences, often times failures in mathematics, usually dictate student opinions concerning their perception of their ability in mathematics as well as their optimism about career choices where mathematics is a basis of the curriculum ... ultimately their futures are limited to areas where mathematics is rarely used" (Hall & Ponton, 2002, p.10). While the Third International Mathematics and Science Survey (TIMMS - 1998-1999) reports that New Zealand students at Year 9 level achieve in mathematics at about the international mean (Chamberlain & Caygill, 2002), evidence also highlights a high number of New Zealand fourteen year olds scoring below international benchmarks in mathematics (Maxim Institute, 2003). In the Report by Maxim Institute, 44% of New Zealand 14 year olds are reported to score below fixed international benchmarks in mathematics "...and means that approximately 31,000 of 70,000 Year 9 pupils are 'unable to apply basic mathematical knowledge in straightforward situations' " (p.20). Self-efficacy plays a critical in educational achievement, and in mathematics achievement (Pajares, 1996; Pajares & Miller, 1997; Pajares & Valiante, 1997; Stevens, Olivarez, Lan & Tallent-Runnels, 2004). "Compared with students who doubt their learning capabilities, those who feel efficacious for learning or performing a task participate more readily, persist longer when they encounter difficulties, and achieve at a higher level" (Schunk, 1994, p.75 ).
This present research is part of a two-phased study which aimed to assess self-efficacy and agency in mathematics of diverse students from multicultural secondary schools in Auckland. The measures which were developed, also included items and subscales adapted from Bandura (2001a); and Pintrinch (1986). The measures were tailored to assess self-efficacy for mathematics in the context of the general aims of mathematics education and achievement aims of the mathematics curriculum as listed in the New Zealand curriculum framework (Ministry of Education, 1992). The seven aims have been subgrouped into three categories (Ferguson, 2002). These include: (a) personal aspects related to students' confidence in their ability to undertake mathematics tasks, and belief in the value of mathematics, (b) developing knowledge and skills in content and thinking processes, and (c) the relevance of mathematics to higher studies and work. These three indices emphasise the different domains of self-efficacy cognitive, behavioural, and emotional. The curriculum framework also enumerates the eight essential skills: (a) communication, (b) numeracy; (c) information; (d) problem-solving; (f) self-management and competitive skills; (g) social and co-operative skills; (i) physical skills; and (j) work and study skills. These eight skills have been interwoven in the six major strands into which the achievement aims of mathematics education have been grouped. These include: (a) mathematical processes, (b) number, (c) measurement, (d) geometry, (e) algebra, and (f) statistics. To the last three strands, a few changes have been made to the Curriculum Framework related to Level 8 (Ministry of Education, 1995). These six strands were used as the main framework in designing the mathematics self-efficacy scale. Using multi-faceted predictors of self-efficacy, subscales of the following related constructs were incorporated. These included self-efficacy in: (a) motivation, (b) cognitive learning strategies, (c) self-regulation, (d) resource management, (e) leisure-time skills and extracurricular activities, (f) enlisting support, and (g) self-assertiveness. Emotional self-efficacy was measured through items in subscales on cognitive strategies, cognitive self-regulation, leisure time and extracurricular activities. The items within subscales were designed such that the three dimensions of level, generality and strength of self-efficacy were taken into consideration. This paper reports the findings of the first phase of the study which assessed self-efficacy in mathematics of diverse students from multicultural schools in Auckland.
Part I included six sections, each assessing self-efficacy in mathematics on a range of specified dimensions. (See Appendix for Part I of the scale-based questionnaire). Part II, (section VII) sought demographic data. Participants were requested to provide information on gender, ethnicity, age-group, family structure, languages spoken, choice of subjects, favourite subject/s, and likelihood of taking up tertiary education following bursary examinations.
| Item subscales | alpha |
| Numerical problems and measurement | .83 |
| Geometry | .77 |
| Algebra | .81 |
| Statistics | .81 |
| Mathematical processes | .82 |
| Motivation | .94 |
| Cognitive strategies | .96 |
| Resource Management | .93 |
| Self-regulated learning | .96 |
| Leisure time skills | .93 |
| Meeting others expectations | .95 |
| Self assertiveness | .94 |
| Section I - Numerical problems and measurement - 6 items; Section II - Geometry - 2 items; Section III - Algebra - 4 items; Section IV - Statistics - 3 items; Section V - Mathematical processes - 6 items; Section VI - Some items in the subscales in section VI were self-designed, and others adapted from published measures (Bandura, 2001a; Pintrinch, 1986). | |
Subscales included: Motivation strategies (5 items); cognitive strategies (15 items); resource management strategies (12 items); self-regulated learning (16 items); leisure time skills and extracurricular activities (6 items); self-belief to meet others expectations (4 items); self-assertiveness (6 items). All items required participants to respond to a Likert 5 point scale ranging from 'not well at all' to 'very well'. The midpoint was 'satisfactorily'. The participation rate was 64%. Out of 215 questionnaires distributed, there were 137 returns. Participants rated their self-efficacy in the 'satisfactory' to 'pretty well' range indicating moderately high levels of self-efficacy. The means and standard deviation of responses of participants are shown in Table 2.
| Subscales | Item Means |
Scale Means | Scale SD |
| Self-efficacy in numerical problems and problems of measurement | 3.30 | 19.79 | 4.45 |
| Self-efficacy in geometry | 3.13 | 6.25 | 1.51 |
| Self-efficacy in algebra | 3.02 | 12.10 | 2.84 |
| Self-efficacy in statistics | 3.21 | 9.63 | 2.25 |
| Self-efficacy in mathematical processes | 3.35 | 20.11 | 4.86 |
| Self-efficacy in motivational strategies | 3.43 | 17.17 | 6.28 |
| Self-efficacy in cognitive strategies | 3.32 | 49.78 | 17.10 |
| Self-efficacy in resource management strategies | 3.31 | 39.71 | 14.41 |
| Self-efficacy in self-regulated learning | 3.33 | 53.31 | 18.01 |
| Self-efficacy in leisure time skills | 3.68 | 22.06 | 8.75 |
| Self-efficacy to meet others expectations | 3.60 | 14.40 | 5.61 |
| Self-efficacy for self-assertiveness | 3.82 | 22.93 | 8.07 |
Correlations were computed between subscales based on Pearson's Product Moment correlation. All correlations between subscales in the mathematics self-efficacy subsection were significant and positive. The range was between .58 and .68 (p<.01). Correlations were significant and positive between subscales on related constructs, with a few exceptions. Positive, and significant correlations ranged between .29 and .87 (p<.01). Correlations between subscales in self-efficacy for mathematics and the other subscales showed positive and mostly significant correlations ranging between a low .11 and .56.
Following correlation, factor analyses (Varimax rotated, based on principal component analysis) were computed. The aim was to explore the possibility of categorising the subscales based on emerging factors. Table 3 shows the 3 factors which accounted for 67% of the variance. The three factors can be categorised as follows:
| Subscales | Factors | ||
| 1 | 2 | 3 | |
| Self assertiveness | .881 | ||
| Meet others expectations | .836 | .307 | |
| Leisure time skills | .815 | ||
| Self regulated learning | .750 | .471 | |
| Numerical problems | .750 | .326 | |
| Geometry | .747 | ||
| Math processes | .616 | ||
| Algebra | .607 | ||
| Statistics | .606 | ||
| Cognitive strategies | .329 | .841 | |
| Motivation strategies | .303 | .731 | |
| Resource Management | .539 | .572 | |
| Eigenvalue | 3.28 | 2.50 | 2.3 |
| Variance | 27.34 | 20.84 | 19.35 |
In the next stage of data analyses, achievement scores were analysed using both descriptive and inferential procedures. Pearson's Product Moment Correlations were computed between factor scores and academic achievement scores (See Table 4).
| Factors | Achievement | Factor 1 | Factor 2 | Factor 3 |
| Achievement | 1.0 | .14 | .045 | .138 |
| Factor 1 | .14 | 1.0 | .49** | .82** |
| Factor 2 | .04 | .49** | 1.0 | .58** |
| Factor 3 | .14 | .82** | .58** | 1.0 |
| **Correlation significant at p<.01 level. | ||||
See figure 1 for a path framework of the tabular data.
Achievement scores correlated positively but at a low level with the three factors. It is important to note that the categorisation of achievement scores was based on ordinal ranking, taking into consideration the overall trend in achievement of students in the two schools. (See Table 5 for summary of academic achievement results in mathematics).
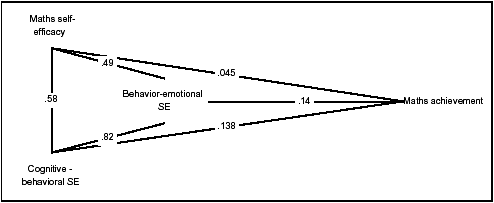
Figure 1: Path framework of the three factors with achievement
| Grade | Frequency (%) |
| Excellence | 16.00 |
| Merit | 9.00 |
| Achieved | 21.05 |
| Not achieved | 42.70 |
| Did not sit | 11.25 |
| n=137 | |
To test the variables which predict differences in academic achievement, and to assess the relative importance of the independent variables, multiple discriminant analysis (MDA) was used. The F test of Wilks's lambda shows the relative contribution of the different independent variables (See Table 6). As can be seen the correlations were high but not significant.
Analysis of the canonical discriminant functions table shows the four main discriminating functions. Table 7 shows that Function 1 accounts for 51.6% of the variance, and Function 2 accounts for 25.6% of the variance. The canonical correlation which is the ratio of between-groups variance to the total variation, is highest for Function 1, whereby one can conclude that this function explains most of the variance. The structure matrix helps ascertain the correlation of each of the independent variables with the Functions. The pooled within-group correlations between the discriminating variables and the canonical discriminant functions can be seen in Table 8. These can be considered similar to factor loadings. The variables which have high loadings in each function
| Wilks' lambda | F | df1 | Df2 | Sig | |
| Numerical problems | .958 | 1.395 | 4 | 126 | .239 |
| Geometry | .974 | .843 | 4 | 126 | .500 |
| Algebra | .926 | 2.505 | 4 | 126 | .045 |
| Statistics | .981 | .596 | 4 | 126 | .666 |
| Math processes | .930 | 2.374 | 4 | 126 | .056 |
| Motivation | .972 | .895 | 4 | 126 | .469 |
| Cognitive strategies | .984 | .526 | 4 | 126 | .717 |
| Resource management | .939 | 2.058 | 4 | 126 | .090 |
| Self-regulated learning | .967 | 1.078 | 4 | 126 | .370 |
| Leisure time skills | .964 | 1.165 | 4 | 126 | .329 |
| Self-assertiveness | .967 | 1.058 | 4 | 126 | .380 |
| Ability to meet expectation | .939 | 2.045 | 4 | 126 | .092 |
are the main variables which predict differences between the groups. In the results of the present study these variables are self-efficacy in resource management strategies, self-efficacy in algebra, self-efficacy to meet others' expectations, and self-regulatory self-efficacy. For Function 2 all variables which are significant are from the mathematics curriculum-specific self-efficacy scale. The self-efficacy scales on leisure-time skills, self-assertiveness, meeting others' expectations, and self-regulated learning show highly significant loadings on Function 4. Function 2 and Function 4 have loadings of variables which show significant correlations which are similar to those in Factors 1 and 2, as can be seen in the results of factor analyses.
| Functions | Eigenvalue | % of variance | Cumulative % | Canonical Correlation |
| 1 | .235 | 51.5 | 51.5 | .437 |
| 2 | .117 | 25.6 | 77.1 | .324 |
| 3 | .055 | 12.1 | 89.2 | .229 |
| 4 | .049 | 10.8 | 100.0 | .217 |
The standardised canonical discriminant coefficients which calculate predicted groupings of participants can be seen in Table 9. This data can be interpreted in the light of the means for each of the participant groups. See Table 10 and Table 11.
| Scales | Function | |||
| 1 | 2 | 3 | 4 | |
| Resource management | .503(*) | .016 | -.222 | .250 |
| Maths processes | .183 | .723(*) | -.262 | .217 |
| Numeracy | .139 | .578(*) | .063 | .083 |
| Algebra | .443 | .498(*) | .276 | .002 |
| Geometry | -.107 | .450(*) | -.057 | -.049 |
| Motivation | .200 | .375(*) | -.148 | -.163 |
| Stats | .183 | .299(*) | -.002 | .099 |
| Cognitive strategies | .171 | .260(*) | .179 | .039 |
| Leisure time skills | -.002 | -.001 | -.076 | .861(*) |
| Self-assertiveness | .198 | .153 | -.091 | .654(*) |
| Meeting expectations | .441 | .191 | .048 | .546(*) |
| Self-regulated learning | .307 | .091 | .018 | .473(*) |
| Pooled within-groups correlations between discriminating variables and standardised canonical discriminant functions. Variables ordered by absolute size of correlation within function. *Largest absolute correlation between each variable and any discriminant function. | ||||
| Scales | Function | |||
| 1 | 2 | 3 | 4 | |
| Numeracy | -.235 | .120 | .241 | .133 |
| Geometry | -.530 | -.009 | -.088 | -.278 |
| Algebra | .557 | .254 | .571 | .218 |
| Statistics | .216 | -.227 | .167 | -.138 |
| Maths processes | .011 | 1.123 | -.667 | .256 |
| Motivation | -.088 | .068 | -.890 | -.503 |
| Cognitive strategies | -.319 | -.127 | 1.336 | -.112 |
| Resource management | 1.014 | -.985 | -.956 | -.102 |
| Self-regulated learning | -.790 | .289 | .499 | .060 |
| Leisure-time skills | -.488 | -.363 | -.023 | .896 |
| Self-assertiveness | -.249 | .145 | -.394 | .236 |
| Meeting others expectations | 1.226 | .206 | .341 | -.135 |
| Ach Scores | Function | |||
| 1 | 2 | 3 | 4 | |
| Not achieved | -.310 | .213 | -.215 | .038 |
| Achieved | -.475 | -.269 | .276 | -.033 |
| Merit | .553 | -.519 | -.261 | -.399 |
| Excellence | .588 | .440 | .236 | -.089 |
| Did not sit | .634 | -.378 | -.039 | .534 |
| Unstandardised canonical discriminant functions evaluated at group means. | ||||
| Subscales | Not achieved | Achieved | Merit | Excellence | Did not sit |
| Numeracy | 20.02 | 18.91 | 18.64 | 21.13 | 19.38 |
| Geometry | 6.52 | 6.19 | 5.93 | 6.50 | 5.92 |
| Algebra | 11.92 | 11.44 | 11.93 | 13.63 | 12.38 |
| Statistics | 9.67 | 9.25 | 9.43 | 10.17 | 9.77 |
| Maths processes | 20.98 | 18.53 | 18.86 | 21.83 | 20.08 |
| Motivation | 17.35 | 15.75 | 17.21 | 18.63 | 16.54 |
| Cognitive strategies | 48.58 | 47.56 | 47.57 | 52.88 | 49.46 |
| Resource management | 37.73 | 35.19 | 41.50 | 41.50 | 44.15 |
| Self-regulated learning | 51.79 | 49.84 | 51.64 | 55.79 | 59.54 |
| Leisure time skills | 22.25 | 21.44 | 19.14 | 21.04 | 25.69 |
| Self-assertiveness | 22.94 | 21.41 | 21.21 | 23.63 | 26.08 |
| Meeting others expectations | 13.85 | 12.91 | 13.86 | 15.92 | 16.92 |
The means of each of the groups help us interpret the difference among the groups. For example, those who have done excellently, and achieved with merit show high means in Function 1 which had high correlations for self-efficacy in resource management strategies, algebra, ability to meet others' expectations, and self-regulatory learning. The participants in the excellence group also have high means on Function 2. The variables in Function 2 which had the highest and significant correlations were the mathematics self-efficacy scales, and scales on cognitive strategies and motivation. The 'not achieved' group had low means on Functions 1, 2, 3, and 4. Interestingly those who did not attempt the exams also reported high means on Functions 1 and 4.
The major findings emerging from the data analysis of this current research are as follows:
Outcome expectations and valuing the learning task are also factors to be considered which could have impacted on participants' reported level of self-efficacy. Dornyei (2001) cautions that self-efficacy beliefs are only indirectly related to actual competence and abilities because they are a complex process of self-persuasion that is based on cognitive processing of diverse sources of information. Tschannen-Moran, Hoy and Hoy (1998) state that self-efficacy has to do with the self-perception of competence; it is not the actual level of competence. In situations where misjudgment is perceived as inconsequential, there is likely to be less serious appraisal of self-efficacy (Bandura, 1997). Cramer (1998) states that self-reporting "positive illusions" about the self, giving responses which might be socially desirable are coping strategies. Reviewing studies on the use of overly positive self-evaluations, and self-deceptive coping in college students, Cramer argues that when the outcome measure is an external criterion and not self-reports, use of coping mechanisms such as these do not result in positive benefits. This was very evident in the study. While participants reported high levels of self-efficacy, the level of performance attainment was low.
Factors impacting adversely on student achievement have been highlighted by the evaluation reports on school improvement initiatives in multicultural schools in New Zealand. Self-esteem and motivation were two aspects identified as impacting on New Zealand students' ability and achievement (Sinclair, Bates, & Gavin, 2001). Hill and Hawke (1998) highlight lack of control over external factors such as poverty, health, housing, employment, and family affecting adversely on learning opportunities and student achievement. In reviewing the New Zealand Curriculum, Donnolley (2002) states that the objective underpinning the statement of raising achievement of all students and ensuring that the quality of teaching and learning is of the highest international standards has not been achieved. The major highlight of the review is the suggestion to replace the outcomes-based approach to the curriculum with a 'standards' or 'syllabus' based approach. He states that this process based approach fails to recognise the significance of educational content. In a similar critique on the New Zealand education scene, Hames (2002) questions the emphasis of the educational system on self-esteem, at the cost of equipping students with the required knowledge of content and skills. He quotes the views of a teacher from Rotorua who taught students from deprived backgrounds, "[A] school does need compassionate and visionary leadership to lead students out of problems. But if that support is provided, in the end self-esteem is not an excuse for poor performance" (p.49).
It emerges that there is a need to explore the teaching-learning context in terms of the strategies of learning used in the classroom. Investigating the causal role of students' self-efficacy, self-set goals and use of learning strategies on academic grades in school settings, Zimmerman, Bandura, and Martinez-Pons (1992) hypothesised that students' perceived self-regulatory efficacy would impact on self-efficacy for academic achievement, which in turn would influence goal setting and grades attained. Results revealed that efficacy for self-regulated learning and academic achievement, and actual attainment were causally linked. Students who had high self-regulatory efficacy were more confident of subject mastery and attaining desired performance. Personal goals were crucial in attaining grades. The higher the perceived self-efficacy, the higher the set goals, and level of attaining the goals. The teaching strategies used in the classroom were investigated in a study by the New Zealand Educational Review Office (ERO) in 2002. The ERO Report aimed to identify the ways in which mathematics teachers of Years 1 to 8 students developed teaching programs from the achievement objectives of the mathematics curriculum statements, how they used the problem-solving approach in teaching, and the extent to which small group teaching strategies were used. The philosophy underlying the problem-solving approach was that as advocated in the Netherlands (Schoenfeld, 1992), by working on realistic problems students would develop an understanding of mathematical concepts. Teacher interviews revealed that the most favoured strategies were whole class teaching at the initial phase of teaching, based on modelling of the new concept, followed by group practice to apply the new learning. Concrete examples and materials were use to aid understanding. Although there was likely to be some form of assessment to ascertain whether the students had achieved the learning outcomes, it was not clear whether there was feedback on the effectiveness of the strategies on a regular basis. Most of the teachers preferred the procedure of whole-class teaching, modelling, followed by group activities, and use of concrete examples to teach new concepts in mathematics. The Report recommends more research on group teaching in New Zealand, on the advantages of whole-class teaching, and on teaching strategies to facilitate teachers to make informed decisions on choice of appropriate strategies. Teacher effects emerge as a significant variable impacting on student achievement in New Zealand (Alton-Lee, 2003b). The second phase of this research investigates students' beliefs in the use of specific learning strategies in mathematics. Teachers' beliefs in the use of strategies of learning, which is a major source of agency, is also explored. The findings from the second phase will be reported in a subsequent paper.
Since there is a demonstrated relationship between self-efficacy and academic achievement of students, the following recommendations can be considered to enhance mathematics self-efficacy and academic achievement through relevant teaching-learning interventions. Based on life-centred psychological principles, and teaching-learning principles in a multi-cultural context (American Psychological Association, 1997; Banks, Cookson, Gay, & Hawley, 2001; Bishop, Berryman, Tiakiwai, & Richardson, 2003; Centre for Positive Research Practices, 2003), it is proposed that these recommendations will enrich the New Zealand teaching-learning context.
Alton-Lee, A. (2003b). Impact of teaching and schools on variance in outcomes. Wellington: Ministry of Education.
American Psychological Association (APA) (1997). Learner-centred psychological principles: A framework for school redesign and reform. Revision prepared by a Work group of the American Psychological Association's Board of Educational Affairs (BEA) (2003). Retrieved from http://www.apa.org/ed/lcp.html on 17/11/2003
Ames, C. A. (1990). Motivation: What teachers need to know. Teachers College Record,91(3), 409-421.
Bandura, A. (1977). Self-efficacy: Toward a unifying theory of behavioral change. Psychological Review, 191-215.
Bandura, A. (1986). Social Foundations of thought and action: A social cognitive theory. New Jersey: Prentice-Hall Inc.
Bandura, A. (1990). Self-regulation of motivation and action through anticipatory self-reactive mechanisms. Presented to the Nebraska Symposium on Motivation, Nebraska.
Bandura, A. (1997). Self-Efficacy: The exercise of control. USA: W. H. Freeman and Company.
Bandura, A. (1999). Social cognitive theory of personality. In L. A. Pervin & O. P. John (Eds.), Handbook of personality (pp. 154-196). New York: The Guilford Press.
Bandura, A. (2000). Exercise of human agency through collective efficacy. American Psychological Society, 9(3), 75-78.
Bandura, A. (2001a). Guide for constructing self-efficacy scales. Retrieved from: http://www.emory.edu/education/mfp/eg.html. December 2001.
Bandura, A. (2001b). Social cognitive theory: An agentic perspective. Annual Review of Psychology, 52, 1-26.
Bandura, A. (2002). Social cognitive theory in cultural context. Applied Psychology: An International Review, 51(2), 269-290.
Bandura, A. & Cervone, D. (1986). Differential engagement of self-reactive influences in cognitive motivation. Organisational Behaviour and Human Decision Processes, 38, 98-113.
Banks, J. A., Cookson, P., Gay, G. & Hawley, W. D. (2001). Diversity within unity: Essential principles for teaching and learning in a multicultural society. Phi Delta Kappan, 83(3), 196-203.
Bempechat, J. & Drago-Severson, E. (1999). Cross-national differences in academic achievement: Beyond etic conceptions of children's understandings. Review of Educational Research, 69(3), 28-314.
Bishop, R., Berryman, M., Tiakiwai, S. & Richardson, C. (2003). Te Kotahitanga: The experiences of Year 9 and 10 Maori students in mainstream classrooms (Report to Ministry of Education). Wellington: Ministry of Education.
Centre for Positive Practices (undated, updated 2003). Interventions enhancing self-efficacy. Retrieved from http://www.positivepractices.com/Efficacy/InterventionsEnhancingSel.html on 10/10/2003
Chamberlain, M. & Caygill, R. (2002). The school and classroom context for Year 9 students' mathematics and science achievement (Report to Ministry of Education). Wellington: Ministry of Education.
Chye, S., Walker, R. A. & Smith, I. D. (1997). Self-regulated learning in tertiary students: The role of culture and self-efficacy on strategy use and academic achievement. Paper presented at the Australian Association for Research in Education Conference. http://www.aare.edu.au/97pap/chyes350.htm
Coakes, S. J. & Steed, L. G. (1999). SPSS: Analysis without anguish. Queensland: John Wiley & Sons Ltd.
Covington, M. V. (2000). Goal theory, motivation, and school achievement: An integrated review. Annual Review of Psychology, 51, 171-200.
Cramer, P. (1998). Coping and defense mechanisms: What's the difference? Journal of Personality, 66(6), 919-946.
Donnolley, K. (2002). A review of New Zealand's curriculum: An International perspective (Report to: Education Forum).
Dornyei, Z. (2001). Teaching and researching motivation. Essex: Pearson Education Ltd.
Education Review Office (2000). Multi-cultural schools in New Zealand. Wellington: ERO. [14 Oct 2003] http://www.ero.govt.nz/Publications/pubs2000/MulticulturalSchools.htm
Ferguson, G. A. & Takane, Y. (1989). Statistical analysis in psychology and education. New York: McGraw Hill Book Company.
Ferguson, S. (2002). Curriculum stocktake: Report on the New Zealand National Curriculum, 2002. Wellington: The Ministry of Education.
Furnham, A. (2000). Attitudes towards homeopathy in particular beliefs about contemporary medicines in general. Psychology, Health & Medicine, 5(3), 327-342.
Gibson, C. B. (1999). Do they do what they believe they can? Group efficacy and group effectiveness across tasks and cultures. Academy of Management Journal, 42(2), 138-152.
Hill, J. & Hawke, K. (1998). Achievement is cooler than it was: Achievement in multi-cultural high schools. Wellington: Massey University.
Hall, M. & Ponton, M. (2002). A comparative analysis of mathematics self-efficacy of developmental and non-developmental freshman mathematics students. Presented at the meeting of Louisiana / Mississippi section of the Mathematics Association of America.
Hames, M. (2002). The crisis in New Zealand schools. Palmerston North: The Education Forum.
Kranzler, J. H. & Pajares, F. (1997). An exploratory factor analysis of the mathematics self-efficacy scale -revised (MSES - R). Measurement and Evaluation in Counselling and Development, 29(4), 215-228.
Maddux, J. E. (Ed.). (1995). Self-Efficacy theory: An introduction. New York: Plenum Press.
Maxim Institute (2003). In harm's way: Educational achievement of New Zealand pupils - an international comparison. Auckland: Maxim Institute.
Ministry of Education. (1995). Mathematics in the New Zealand curriculum. Wellington: Learning Media Limited.
Ministry of Education. (1992). Mathematics in the New Zealand curriculum. Wellington: Learning Media Limited.
New Zealand Government. (2001a). Ko e Ako 'a e Kakai Pasifika The strategy for Pacific education. Wellington: Ministry of Education. Retrieved from http://www.minedu.govt.nz/ March 2002
New Zealand Government. (2001b). New Zealand school statistics. Wellington: Ministry of Education. Retrieved from http://www.minedu.govt.nz/ March 2002
O'Brien, V., Martinez-Pons, M. & Kopala, M. (1999). Mathematics self-efficacy, ethnic identity, gender, and career interests related to mathematics and science. The Journal of Educational Research, 92(4), 231-235.
Oettingen, G. (1995). Cross-cultural perspectives on self-efficacy. In A. Bandura (Ed.), Self-Efficacy in changing societies (pp. 149-176). Cambridge: Cambridge University Press.
Pajares, F. (1996). Self-efficacy beliefs in academic settings. Review of Educational Research, 66(4), 543- 578.
Pajares, F. & Miller, M. D. (1997). Mathematics self-efficacy and mathematical problem solving: Implications of using different forms of assessment. Journal of Experimental Education, 65(3), 213-229.
Pajares, F. & Valiante, G. (1997). Influence of self-efficacy on elementary students' writing. The Journal of Educational Research, 90(6), 353-361.
Patrick, H., Hicks, L. & Ryan, A. M. (1997). Relations of perceived social efficacy and social goal pursuit to self-efficacy in academic work. Journal of Early Adolescence, 17(2), 109-128.
Peers, I. (1996). Statistical analysis for education & psychology researchers. London: Falmer Press.
Pintrinch, P. R. (1986). Motivation strategies for learning questionnaire. USA: The University of Michigan.
Pintrinch, P. R. & Schunk, D. H. (2002). Motivation in education: Theory, research, and applications. (2nd ed.). New Jersey: Merrill Prentice Hall.
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334-370). Canada: MacMillan; Maxwell MacMillan.
Schunk, D. H. (1994). Self-regulation of self-efficacy and attribution in academic settings. In D. H. Schunk & B. J. Zimmerman (Eds.), Self-regulation of learning and performance: Issues and educational implications (pp. 75-99). New Jersey: Lawrence Erlbaum Associates, Inc.
Schunk, D. H. (1995). Self-efficacy and education and instruction. In J. E. Maddux (Ed.), Self-efficacy, adaptation, and adjustment: Theory, research, and application (pp. 281 -303). New York: New York.
Schunk, D. H. (2000). Learning theories: An educational perspective. New Jersey: Prentice-Hall, Inc.
Schunk, D. H. & Ertmer, P. A. (1994). Self-regulation of learning and performance. In D. H. Schunk & B. Zimmerman (Eds.), Self-regulation of learning and performance (pp. 631-649). New Jersey: Lawrence Erlbaum Associates, Inc.
Sinclair, M., Bates, T. & Gavin, B. (2001). AIMHI Project: Case study, Pacific Vision International Conference - Identity and Education BS25. New Zealand.
Stevens, T., Olivarez, A., Lan, W. Y. & Tallent-Runnels, M. K. (2004). Role of mathematics self-efficacy and motivation in mathematics performance across ethnicity. The Journal of Educational Research, 97(4), 208-221.
Tschannen-Moran, M., Hoy, A. W. & Hoy, W. K. (1998). Teacher efficacy: Its meaning and measure. Review of Educational Research, 68(2), 202-248.
Zimmerman, B. J. (1995). Self-efficacy and educational development. In A. Bandura (Ed.), Self-efficacy in changing societies (pp. 202-231). Cambridge: Cambridge University Press.
Zimmerman, B. J. (2002). Becoming a self-regulated learner: An overview. Theory into Practice, 41(2), 64- 70.
Zimmerman, B.J., Bandura, A. & Martinez-Pons, M. (1992). Self-motivation for academic attainment: The role of self-efficacy beliefs and personal goal setting. American Educational Research Journal, 29(3), 663-676.
| How well do you believe you can calculate accurately numerical problems mentally? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can calculate accurately numerical problems on paper? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can estimate and make approximations? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can interpret the accuracy of results and measurements? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can calculate the effects of change in variables using mathematical models? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can predict the rate of change of variables using mathematical models? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| Given below is a problem, which you have the option to attempt or not
Shrubs are planted in a row with their centres 3 m apart. The shrubs are 1m wide and grow in width at a rate of 20 cm every year. |
 The shrubs will touch each other after: |
SECTION II OF VII
The focus is in your belief in your capability to attempt successfully problems in GEOMETRY
| How well do you believe you can recognise the geometrical properties of objects in daily life? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can use geometrical models to solve practical problems in daily life? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
Given below is a problem, which you have the option to attempt or not
1. sin 150° has the same value as: (circle your choice)
|
SECTION III OF VII
The focus is on your belief in your capability to attempt successfully problems in ALGEBRA
| How well do you believe you can recognise patterns and relationships in mathematics and generalise from these? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can think abstractly and use symbols to communicate mathematical concepts, relationships and generalisations? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can think abstractly and use graphs and diagrams to communicate mathematical concepts, relationships and generalisations? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can use algebraic expressions to solve practical problems? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| Given below is a problem, which you have the option to attempt or not
Simplify: 5a - 2b - 8a + 7b = _______ |
SECTION IV OF VII
The focus here is about your belief in solving problems in STATISTICS.
| How well do you believe you can analyse statistical data as reports and summaries? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can interpret data presented in charts, tables and graphs? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can estimate probabilities? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
SECTION V OF VII
The focus here is about your belief in using mathematical processes
| Given below is a problem, which is optional.
The formula used to convert degree Celsius, C, into degrees Fahrenheit, F, is F =9/5 C+32 30 Celsius is equal to: |
| How well do you believe you can use logical and systematic thinking in mathematical contexts? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| In a mathematical problem solving situation, how well do you believe you can critically reflect on the method you have chosen? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can use information technology in mathematical contexts? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can be part of a problem solving team, expressing your ideas, listening and responding to others? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can use the knowledge and skills in mathematics to interpret presentations of mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
(The following question is to be attempted only by those students who are bilingual i.e. use their ethnic language for communication on a daily basis at home. Other participants can kindly proceed to the next question)
| How well do you believe you have developed skills in using your own ethnic language to express mathematical ideas? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
SECTION VI OF VII
(Please note that questions are mathematics- specific and also applicable in general. Hence some might seem repetitive.)
| How well do you believe you can study in appropriate ways that you will be able to learn mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe that if you try hard enough you will be able to understand the different concepts in mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe that you understand the most complex concepts in mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe that you can master the skills taught in mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe that you can do an excellent job on the assignments and tests in mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can set goals for yourself to direct your activities? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When you study mathematics how well do you believe you can outline the material to help organise your thoughts? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When you study mathematics how well do you believe you can formulate questions to focus your thoughts? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can go through your notes and readings to find out the most important concepts? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying a new mathematical concept how well do you believe that you can skim it to see how it is organised? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can think through the topic to decide what it is you are supposed to learn rather than just reading it over? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe that you can use information from different sources such as class notes, text books and discussions? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe that you can ask yourself questions to make sure that you have understood the material? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe that you can change the way of study to fit the requirements of the topic? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can memorise key words to help recall important concepts? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can summarise concepts of the topic of study? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can determine the concepts you have not understood well? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can relate ideas from mathematics to other subject/s? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can try to relate material to what you already know? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| When studying mathematics how well do you believe you can sort out confusion which arises over missing note taking in class? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well can do you believe you can explain a topic in mathematics to your classmate/ friend? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can work on your own, even if you have trouble learning the material in mathematics class? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can use your study time for mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can work with your classmates to complete the course assignments? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can work in class even if you don't like what is being done? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can stick to your study schedule? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can seek clarifications from your mathematics teacher when you do not understand a concept? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can persist on a topic in mathematics when you find the material difficult? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can ask a peer/ another student in class for help in mathematics when you cannot understand the material being taught? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can keep up with topics and assignments in mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can manage to keep working in mathematics even when you find the material uninteresting? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can review your mathematics notes / readings before an exam? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can finish your mathematics homework assignments by deadlines? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can learn mathematics when there are other interesting things to do? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can concentrate on school subjects? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can concentrate in mathematics in the classroom? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well can do you believe you can take notes of class instruction? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can take notes of mathematics during class instruction? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can use the library to get information for class assignments? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can plan your school work? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can organise your school work? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can remember information presented in class and textbooks? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can remember information presented in class and textbooks in mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can arrange a place to study without distractions? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can motivate yourself to do school work? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can motivate yourself to do school work in mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can participate in class discussions? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can clarify doubts in mathematics in class? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can learn sport skills? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can learn dance skills? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can learn music skills? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can do the kinds of things needed to be a member of the school newspaper? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can do the things needed to be a member of the students' council? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you learn the skills for team sports (for example basket ball, volleyball, swimming, cricket, rugby)? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can live up to what your parents expect of you? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can live up to what your teachers expect of you? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can live up to what your mathematics teacher expect of you? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can you live up to what your peers expect of you? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can express your opinions when other classmates disagree with you? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can live up to what you expect of yourself in mathematics? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can you stand up for yourself when you feel you are being treated unfairly? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can stand firm to someone who is asking you to do something unreasonable or inconvenient? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can live up to what you expect of yourself? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| How well do you believe you can deal with situations when others are annoying you or hurting your feelings? | ||||
| 1 Not well at all | 2 Not too well | 3 Satisfactorily | 4 Pretty well | 5 Very well |
| Author: Deepa Marat is a doctoral candidate at the Auckland University of Technology. This is the second publication from her doctoral work which is in progress. She works as a Research Assistant at Unitec New Zealand. Her areas of research interests are self-efficacy, self-regulation, motivation, self-appraisal, teacher beliefs, student achievement, and diversity. Email: dmarat@unitec.ac.nz
Please cite as: Marat, D. (2005). Assessing mathematics self-efficacy of diverse students from secondary schools in Auckland: Implications for academic achievement. Issues In Educational Research, 15(1), 37-68. http://www.iier.org.au/iier15/marat.html |