
 |
Does it matter how you measure it? The case of self-efficacy in mathematics
Jehanzeb R. Cheema
University of Illinois, USA
There are many different ways to measure a construct and the method chosen to accomplish this task can have a major effect on results of statistical analyses based on the measured variable. We looked at various methods ranging between naive and sophisticated that can be used to measure self-efficacy within the special context of mathematics, in order to investigate similarities and differences between measurement results. Our conclusion is that under specific situations basic and simple measurements of maths self-efficacy can be as effective as their mathematically elegant but complex counterparts.
However, like most psychological variables self-efficacy is a latent trait that cannot be directly measured and hence must be estimated. This forces one to rely on tools such as survey items in order to measure such self-efficacy (Crocker & Algina, 1986). Item level results can then be used to measure a variable in a variety of ways. These range from simple methods such as taking an average of item scores to sophisticated methods such as using multi-category item response theory (IRT) models, where each method has the potential to generate very different estimates of the latent trait relative to other methods.
For an obvious example, consider what happens when a continuous latent trait is measured as a categorical variable. Had the latent trait been measured as a continuous variable the measurement method would have generated a separate estimate of the latent trait for each case in the sample. On the other hand when that same continuous trait is converted into a categorical variable, valuable information is lost in the process. Where once we had a separate estimate of the latent trait for each case now we are assuming that all individuals within a specific group are completely identical in terms of that latent trait (Gardner, 1975). This example and others like it (e.g. MacDonald & Paunonen, 2002; Teresi, 2006) show that the method of measurement can have a potentially significant effect on the realised shape of the latent trait distribution.
Past studies that have compared results of alternative methods of measurement have generated mixed results with some supporting the use of more sophisticated methods leading to relatively efficient estimates and others highlighting frivolous gains at the expense of added complexity. For example, an earlier analytical study was conducted by Wainer (1976) who showed that simple measurement methods such as unit averaging (or equal weights) have the potential to outperform their relatively sophisticated counterparts that use optimised weights such as ordinary least squares (OLS) regression. Wainer's (1976) results were supported by Dawes (1979) who compared several empirical studies to arrive at the same conclusion, but rejected by Pruzek and Frederick (1978) who suggested that ignoring OLS weights could result in serious and systematic errors of prediction. In a related review of the literature, Raju, Bligic, Edwards, and Fleer (1997) found little support for favouring equal weights regression over its OLS counterpart. However, more recently Waller and Jones (2011) conducted a detailed study using simulated data to analytically show that regression weights rarely matter in scenarios where the objective is to simply predict a criterion of interest from a given set of predictors. Such contrasting findings highlight the lack of consensus in the literature on whether or not relatively sophisticated methods of measurement should be preferred over their computationally less elegant counterparts.
The difference in opinion highlighted in the previous paragraph extends to methods of measurement other than averaging. For example, in an empirical study Fan (1998) used a statewide assessment consisting of a sample of more then 100 items and 193,000 students in order to study the differential effects of ability estimates derived from classical test theory (CTT) and IRT, and found that the two sets of estimates were highly comparable. This conclusion was supported in similar studies by Stage (2003) who used five subsets of Swedish Scholastic Aptitude Test (SewSAT) to show that the gains of switching from CTT to IRT were trivial for test development, and MacDonald and Paunonen (2002) who used a Monte Carlo experiment to investigate the differences in IRT and CTT parameters and arrived at the conclusion that the ability estimates were highly comparable. In a recent study, on the one hand, based on the similarities between factor analytic and IRT-based models Kamata and Bauer (2008) provided analytical formulas for transformation of factor analytic scores into their IRT counterparts and vice versa. On the other hand, instructional pieces such as Hambleton and Russell (1993) and empirical studies such as Progar and Socan (2008) suggest that, when properly employed, IRT estimates tend to be generally empirically superior to their CTT counterparts.
Even if one ignores the controversy and assumes that, at least under specific circumstances, simple measurement methods can be as effective as their relatively more sophisticated counterparts results from past studies tend not to be directly comparable as they are based on different samples of items and participants. Thus, for instance, findings of Dawes (1979) cannot be combined with those of Fan (2008) to say that unit averaging, OLS regression, CTT, and IRT all produce identical estimates. The present study removes this shortcoming by comparing several measurement methods while keeping the set of items and participants constant. In this study we specifically investigate the effect of four measurement methods on self-efficacy in mathematics: equal weighting, principal components extraction, item response theory (IRT) estimation, and ordinal categorisation. In order to reliably isolate the effect of measurement method we use identical samples of items and subjects for each method. To our knowledge to date no other study has investigated the differential effects of measurement methods for self-efficacy in this way.
SE1: Equal weights
This variable represents a linear combination of the eight items measuring self-efficacy in mathematics with each item given an equal weight. The resulting variable had the same scale as the underlying survey items. Denoting item responses with Ii the resulting variable can be expressed by the following equation.
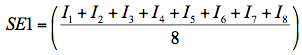 | (1) |
SE2: Principal component extraction
This measurement of self-efficacy is similar to SE1 with the difference that the items were weighted with estimates obtained from a principal components analysis of the eight self-efficacy items. Denoting the principal analysis weight for item i by wi, the measurement can be expressed by the following equation (Tabachnick & Fidell, 2003).
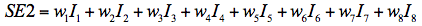 | (2) |
SE3: IRT estimation
Under this method, concepts from item response theory (IRT) were employed to fit a four category partial credit model using the eight self-efficacy items. These kind of IRT models are well suited for items with more than two response categories. Mathematically, this model can be expressed by the following equation (Masters, 1982).
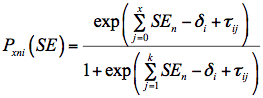 | (3) |
In this expression Pxni(SE) is the probability of person n to score x on item i, SEn is that person's latent self-efficacy, and δi and τij are model parameters. This partial credit model was used to generate an estimate of SEn for each person in the PISA 2003 sample (OECD, 2005; NCES, 2003).
SE4: Ordinal categorisation
For this measure of self-efficacy, we used distribution quartiles of SE2 to divide our sample into four groups of equal size. Following the original item response categories, these groups were labelled: 1 (not at all confident), 2 (not very confident), 3 (confident), and 4 (very confident). Thus, SE4 can be thought of as a categorisation of students based on their cumulative response to the 8 self-efficacy items (i.e. their overall confidence). This method of categorisation is common in experimental research in education and psychology. If we denote the three SE1 quartiles by Q1, Q2, and Q3, then the construction of SE4 can be expressed as follows.
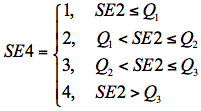 | (4) |
In order to evaluate the relationship between our four self-efficacy variables, we computed Pearson product moment coefficients of correlation between SE1, SE2, and SE3. For the relationship of SE4 with other three self-efficacy variables, we employed Spearman's rank coefficient of correlation. In order to evaluate differences between effects of the four self-efficacy variables when they are employed within a GLM framework, we analysed the simple bivariate relationship between self-efficacy in mathematics and mathematics achievement. The objective here was not to establish a causal relationship between the two variables but to evaluate the effect of different measurement methods considered in this paper. Maths achievement was specifically selected because self-efficacy is known to be a strong predictor of such achievement in the PISA 2003 sample (Kitsantas, Cheema, & Ware, 2011). For this purpose four models were estimated with maths achievement as the dependent variable. The first three models were simple ordinary least squares regression models with SE1, SE2, and SE3 as predictors. The fourth model was an ANOVA model with SE4 as the factor which is equivalent to a regression model of maths achievement on three dummy variables representing SE4. With maths achievement denoted by Y and the dummy variables for SE4 denoted by subscripts 1 through 3, these four models can be expressed by the following equations.
| Model 1: | 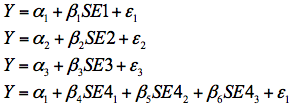 | (5) |
| Model 2: | (6) | |
| Model 3: | (7) | |
| Model 4: | (8) |
The main purpose of fitting these four models was to assess the effect of measurement method for maths self-efficacy on the amount of variation that can be explained in context of a GLM-type model.
For SE1, the eight item responses for each students were combined using the arithmetic mean. Thus, all items had the same weight in the resulting variable with the averaged scores ranging from 1 to 4 (M = 3.13, SD = 0.56). Standardised SE1 ranged between -3.79 and 1.55 (M = 0, SD = 1).
The second method of measurement of self-efficacy involved combining the eight item scores for each student using a linear function obtained from a principal components analysis (PCA) of those items. In order to evaluate whether our dataset was suitable for PCA we evaluated the determinant of correlation matrix, R, the Kaiser-Meyer-Olkin (KMO) test of sampling adequacy, and Bartlett's test of sphericity. The correlation matrix had a non-zero determinant, |R| = 0.05 which means that R-1 exists, the KMO test statistic was .87 which exceeds the usually recommended cut-off of .5 (Tabachnick & Fidell, 2007), and Bartlett's test of sphericity was significant at 5% level of significance, χ2(28) = 16463.68, p < .001. These results suggest that our dataset is suitable for PCA. The PCA was performed using principal axis factoring with the correlation matrix and no rotation. The amount of total variance explained by the extracted component was 43.49% (λ= 4.04) with loadings ranging between .60 and .72 (M = .66, SD .05). For the U.S. sample the standardised component scores for self-efficacy ranged between -3.78 and 0.15 (M = 0, SD = 1).
For SE3, a four category partial credit model based on Masters (1982) was used to derive a self-efficacy estimate for each student. These estimates are included in the PISA 2003 data file (NCES, 2003). For the U.S. sample, the standardised estimated self-efficacy scores ranged between -3.92 and 2.15 (M = 0, SD = 1).
The fourth method of measurement was based on categorising SE2 into approximately four equal groups based on distribution quartiles. A similar method was tried with SE3 but the results remained unchanged. SE1 was not used because given the way that variable was constructed there were only 25 unique averages and a categorisation based on quartiles resulted in group sizes that were very different from each other. The three quartile values for SE2 were Q1 = -.58, Q2 = -.05, and Q3 = .78. Based on these quartile values SE4 was constructed as an ordinal variable with four groups of approximately equal size (not at all confident, 1,350; not very confident, 1,377; confident, 1,364; and very confident, 1,351).
In order to see how various measures of self-efficacy in mathematics are associated with each other Pearson product moment coefficients of correlation were computed for SE1, SE2, and SE3 while Spearman's rank coefficient of correlation was calculated between SE4 and other variables. These correlations are presented in Table 2. All coefficients exceeded .95 and were highly significant, p < .001.
| Items (a) | M | SD | r | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||
| 1. | Using a train timetable to work out how long it would take to get from one place to another | 2.88 | 0.78 | - | ||||||
| 2. | Calculating how much cheaper a TV would be after a 30% discount | 3.15 | 0.77 | .47 | - | |||||
| 3. | Calculating how many square metres of tiles you need to cover a floor | 3.12 | 0.80 | .43 | .56 | - | ||||
| 4. | Understanding graphs presented in newspapers | 3.29 | 0.72 | .40 | .48 | .51 | - | |||
| 5. | Solving an equation like 3x + 5 = 17 | 3.53 | 0.71 | .29 | .40 | .38 | .47 | - | ||
| 6. | Finding the actual distance between two places on a map with a 1:100 scale | 2.80 | 0.88 | .47 | .46 | .50 | .46 | .33 | - | |
| 7. | Solving an equation like 2(x + 3) = (x + 3)(x - 3) | 3.24 | 0.86 | .32 | .40 | .40 | .41 | .68 | .41 | - |
| 8. | Calculating the gas mileage of a car | 3.02 | 0.81 | .40 | .46 | .50 | .41 | .30 | .49 | .35 |
| Note: n = 5,456. Cronbach's alpha = .86. (a) Items have been scaled so that higher values represent more confidence. The four response categories were 1 (not at all confident), 2 (not very confident), 3 (confident), and 4 (very confident). | ||||||||||
The effects of the four measures were further evaluated using simple general linear models to predict maths achievement from maths self-efficacy. In our sample maths achievement ranged from 212.91 to 739.24 (M = 482.88, SD = 92.13). Estimated versions of models defined earlier in equations (5) through (8) are presented in equations (9) through (12) respectively. For model 4 the reference category was group 4 (confident).
| Measure | M | SD | r | ||||
| 1 | 2 | 3 | |||||
| 1. | SE1 | Linear combination of items, simple average | 0 | 1 | - | ||
| 2. | SE2 | Linear combination of items, factor analysis | 0 | 1 | .99 | - | |
| 3. | SE3 | Item response theory estimates | 0 | 1 | .96 | .96 | - |
| 4. | SE4 | Ordinal grouping | .97 | .97 | .97 | ||
| Not at all confident (b) | .25 | - | |||||
| Not very confident | .25 | - | |||||
| Confident | .25 | - | |||||
| Very confident | .25 | - | |||||
| Note: n = 5,456 (a) Pearson r for SE1, SE2, and SE3. Spearman's rank r between SE4 and other variables. (b) For the groups based on SE4, sample size proportion is presented as M. | |||||||
| Estimated model 1: | 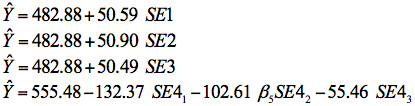 | (9) |
| Estimated model 2: | (10) | |
| Estimated model 3: | (11) | |
| Estimated model 4: | (12) |
In the four estimated models all intercepts, slope coefficients, and partial slope coefficients were significantly different from zero, p < .001. The values of R2 for models 9 through 12 were 30.2%, 30.5%, 30.0%, and 29.4% respectively. These values represent the percentage of variation in maths achievement that can be explained by self-efficacy in the corresponding models. Our main interest in these R2 values was whether or not they were very different from each other. For all practical purposes the variation in this statistic for our sample is trivial.
The sample size used for all statistical results presented in this section was 5,456 and all computations were conducted in SPSS 20 after incorporating proper sampling weights. All tests of hypothesis were evaluated at the 5% level of significance.
Based on statistical results presented in section three, our main finding is that for maths self-efficacy, given the right circumstances, a simple method of measurement such as averaging item scores or categorising observations into groups of equal size can be as effective as mathematically sophisticated methods like principal components analysis and item response theory. We evaluated the similarities and differences between these methods while controlling for the set of survey items and our cases in order to ensure that any observed differences in measures could be directly tied to the measurement method. We found that our four measures of self-efficacy were highly correlated with each other and showed consistent performance in simple GLM models, such as linear regression. These results held remarkably well even when we converted one of our continuous variables into a categorical variable. Such conversion entails a significant loss in information, because all cases falling within a specific group are now assumed to be identical in terms of the latent trait, whereas formerly there existed a separate estimate for each member of that group. This suggests that for samples similar to the one used in this study maths self-efficacy is generally robust to measurement method.
The overall results from the four self-efficacy variables in our study are in remarkable agreement and put a large question mark on the practice of employing advanced methods for scale construction in fields, such as education and psychology. One could argue that unjustified use of such methods introduces unnecessary complexity into applied research, which has the potential to alienate audiences not savvy in quantitative methods. We can certainly say that for the specific case of maths self-efficacy, a simple method such as averaging item scores can provide a high quality variable from reliable well-behaved large samples even when the number of items is as low as eight and the item correlations are only moderate. We hope that our findings will convince applied researchers in education and psychology to have more confidence in simple measurement methods.
For the purposes of this study, we did not allow the set of items underlying self-efficacy to vary. Similarly, our sample remained unchanged. Both of these constraints were essential in order to let us isolate the effect of measurement methods. A change in number or composition of cases or the set of self-efficacy items at the same time as a change in measurement method would have introduced ambiguity making it difficult to isolate the unique effect of measurement method. Although we did not consider these additional sources of variability in our study, future research efforts can be focused in this direction. It would certainly be interesting to see whether or not the findings of our study change if samples of different sizes or a different set of items are used. Other avenues of research include expanding the list of measurement methods, applying the techniques discussed in this paper to other latent traits in education and psychology, and replicating this study with new samples (such as a cross-country analysis).
Bandura, A. (1988). Organizational application of social cognitive theory. Australian Journal of Management, 13(2), 275-302. http://dx.doi.org/10.1177/031289628801300210
Bandura, A. (1993). Perceived self-efficacy in cognitive development and functioning. Educational Psychologist, 28(2), 117-148. http://dx.doi.org/10.1207/s15326985ep2802_3
Crocker, L., & Algina, J. (1986). Introduction to classical & modern test theory. Belmont, CA: Wadsworth Group/Thomson Learning.
Dawes, R. M. (1979). The robust beauty of improper linear models in decision making. American Psychologist, 34(7), 571-582. http://dx.doi.org/10.1037/0003-066X.34.7.571
Fan, X. (1998). Item response theory and classical test theory: An empirical comparison of their item/person statistics. Educational and Psychological Measurement, 58(3), 357-381. http://dx.doi.org/10.1177/0013164498058003001
Fast, L., Lewis, J., Bryant, M., Bocian, K., Cardullo, R., Rettig, M., & Hammond, K. (2010). Does math self-efficacy mediate the effect of the perceived classroom environment on standardized math test performance? Journal of Educational Psychology, 102(3), 729-740. http://dx.doi.org/10.1037/a0018863
Gardner, P. L. (1975). Scales and statistics. Review of Educational Research, 45(1), 43-57. http://dx.doi.org/10.3102/00346543045001043
Hambleton, R., & Russell, J. (1993). An NCME instructional module on comparison of classical test theory and item response theory and their applications to test development. Educational Measurement: Issues and Practice, 12(3), 38-47. http://dx.doi.org/10.1111/j.1745-3992.1993.tb00543.x
Kamata, A., & Bauer, D. J. (2008). A note on the relation between factor analytic and item response theory models. Structural Equation Modeling, 15, 136-153. http://dx.doi.org/10.1080/10705510701758406
Kitsantas, A., Cheema, J., & Ware, H. (2011). Mathematics achievement: The role of homework and self-efficacy beliefs. Journal of Advanced Academics, 22(2), 310-339. http://dx.doi.org/10.1177/1932202X1102200206
Kitsantas A., Ware, H., & Cheema, J. (2010). Predicting mathematics achievement from mathematics efficacy: Does analytical method make a difference? The International Journal of Educational and Psychological Assessment, 5(1), 25-44. https://docs.google.com/file/d/0ByxuG44OvRLPemJWbTVEbHBTSDA
Lewis, J., Ream, R., Bocian, K., Cardullo, R., Hammond, K., & Lisa, F. (2012). Con cariño: Teacher caring, math self-efficacy, and math achievement among Hispanic English learners. Teachers College Record, 114(7), 1-42. http://www.tcrecord.org/library/abstract.asp?contentid=16472
Macdonald, P., & Paunonen, S. V. (2002). A Monte Carlo comparison of item and person statistics based on item response theory versus classical test theory. Educational and Psychological Measurement, 62(6), 921-943. http://dx.doi.org/10.1177/0013164402238082
Masters, G. (1982). A Rasch model for partial credit scoring. Psychometrika, 47(2), 149-174. http://dx.doi.org/10.1007/BF02296272
NCES (2003). National Center for Education Statistics: Program for International Student Assessment [Data file]. Retrieved from http://nces.ed.gov/surveys/pisa/datafles.asp
OECD (2005). PISA 2003 Technical report. Paris, France: Organization for Economic Cooperation and Development. http://www.oecd.org/edu/school/programmeforinternationalstudentassessmentpisa/35188570.pdf
Progar, S. & Socan, G. (2008). An empirical comparison of item response theory and classical test theory. Horizons of Psychology, 17(3), 5-24. http://psy.ff.uni-lj.si/iGuests/Obzorja/Vsebina1/Vol17-3/progar_socan.pdf
Pruzek, R. M. & Frederick, B. C. (1978). Weighting predictors in linear models: Alternatives to least squares and limitations of equal weights. Psychological Bulletin, 85(2), 254-266. http://dx.doi.org/10.1037/0033-2909.85.2.254
Raju, N. S., Bligic, R., Edwards, J. E., & Fleer, P. F. (1997). Methodology review: Estimation of population validity and cross-validity, and the use of equal weights in prediction. Applied Psychological Measurement, 21(4), 291-305. http://dx.doi.org/10.1177/01466216970214001
Stage, C. (2003). Classical test theory or item response theory: The Swedish experience (EM No. 42). Umeå University, Sweden: Publications in Applied Educational Science. http://www.nmd.umu.se/digitalAssets/59/59524_em-no-42.pdf
Tabachnick, G. & Fidell, L. (2007). Using multivariate statistics (5th ed.). Boston, MA: Pearson Education, Inc.
Teresi, J. A. (2006). Overview of quantitative measurement methods: Equivalence, invariance, and differential item functioning in health applications. Medical Care, 44(11), S39-S49. http://www.jstor.org/stable/41219504
Wainer, H. (1976). Estimating coefficients in linear models: It don't make no nevermind. Psychological Bulletin, 83(2), 213-217. http://dx.doi.org/10.1037/0033-2909.83.2.213
Waller, N., & Jones, J. (2011). Investigating the performance of alternate regression weights by studying all possible criteria in regression models with a fixed set of predictors. Psychometrika, 76(3), 410-439. http://dx.doi.org/10.1007/s11336-011-9209-5
Young, W., Weckman, G., & Holland, W. (2011). A survey of methodologies for the treatment of missing values within datasets: Limitations and benefits. Theoretical Issues in Ergonomics Science, 12(1), 15-43. http://dx.doi.org/10.1080/14639220903470205
| Authors: Dr Jehanzeb Cheema is a Clinical Assistant Professor in Education at the University of Illinois at Urbana-Champaign. He received his doctorate in Education in May 2012 from George Mason University. He also received a doctorate in Economics in December 2006 from the University of Wisconsin-Milwaukee. Email: jrcheema@illinois.edu Please cite as: Cheema, J. (2013). Does it matter how you measure it? The case of self-efficacy in mathematics. Issues in Educational Research, 23(3), 346-356. http://www.iier.org.au/iier23/cheema.html |