
 |
The association between secondary mathematics and first year university performance in health sciences
Christopher Joyce, Gregory Hine and Ryan Anderton
The University of Notre Dame Australia
In recent years, there has been a significant decline in the rate of participation in secondary school mathematics courses within Australia, particularly in advanced or higher level mathematics. The aim of this study was to investigate how grade point average (GPA) differed between five health science degrees at an Australian university. The association between Australian Tertiary Admission Ranking (ATAR), the level of mathematics completed at secondary school and GPA was also investigated. Results showed that students studying Biomedical Sciences and Physiotherapy had significantly higher GPA and ATAR than students studying Exercise and Sports Science, Physical Education, and Nursing. A higher percentage of Biomedical Science, and Physiotherapy students undertook advanced mathematics (3C3D MAT) at secondary school than students in the other three degrees, who recorded lower secondary school mathematics result scores from an intermediate or elementary mathematics course studied (3A3B and 2C2D MAT, respectively). The results of this study accord with published literature from other university courses that the decline in numbers of students opting to undertake a higher level of mathematics at secondary school will impact negatively upon their first year university performance.
The aim of this study was to investigate how grade point average (GPA) differed between the five degrees offered in Health Sciences at The University of Notre Dame Australia (Fremantle campus), and if GPA was related to the completed mathematics level at secondary school. In the United States, the use of a GPA to calculate and report academic performance is common practice, and according to Bacon and Bean (2006), GPA has been used as a controlled covariate to gain insights into other relationships across a wealth of studies. In addition to GPA, between-degree differences in the level of mathematics studied at secondary school were also examined.
While the importance of mathematics for tertiary education has been firmly established within the literature base, researchers have also underscored how university success depends on the level of mathematics studied at secondary school (Nicholas, Poladian, Mack & Wilson, 2015). For instance, researchers at an Australian university found considerable differences within a cohort of first-year students enrolled in a health science degree (Hine et al., 2015) and in health sciences degrees (Anderton, Hine & Joyce, 2017). Irrespective of gender, it was determined in both projects that those students who had studied a more difficult mathematics pathway at secondary school attained a significantly higher GPA than those who had taken an easier mathematics pathway. In the United States, Sadler and Tai (2007) suggested that the 'two pillars' supporting academic success within college science are high school study in the same science discipline (e.g. human biology, chemistry) and an advanced study of mathematics. Concerning the latter discipline, these researchers noted that students who take high school calculus average better grades in college science than those who stop at pre-calculus (Sadler & Tai, 2007). Canadian-based research highlighted how the amount of time students spent learning mathematics in their final years of secondary school correlated strongly with their academic performance in a first-year calculus course (Kajander & Lovric, 2005).
In Western Australia, Year 12 students can take as many as six (but no fewer than four) subjects that can be counted towards the Tertiary Entrance Aggregate (TEA). Since 2008, the TEA has been calculated by adding any student's best four scaled subject scores, plus a 10 per cent bonus of a student's best Language Other Than English (LOTE) scaled score. From 2017, students taking mathematics methods and/or mathematics specialist courses will receive a 10 per cent bonus of their final scaled score in those courses, highlighting the recognised importance of studying more difficult mathematics courses. The calculated TEA is then converted to an ATAR, which can range from 0 to 99.95 and reports the ranking position of any student relative to all other students. According to Western Australia's Tertiary Institutions Service Centre (TISC), the ATAR takes into account the number of students who sit the Western Australian Certificate of Education (WACE) examinations in any year, as well as the number of people of Year 12 school-leaving age in the total population (TISC, 2016).
| Course | Elementary | Intermediate | Advanced |
| Number and algebra | (51 hours) - Estimation and calculation - Functions and graphs - Equivalence, equations and inequalities - Finance - Patterns | (58 hours) - Estimation and calculation - Functions and graphs - Equations and inequalities - Patterns - Finance - Calculus | (45 hours) - Estimation and calculation - Functions and graphs - Equations and inequalities - Calculus |
| Measurement and geometry | (20 hours) - Coordinate geometry - Networks - Measurement |
(16 hours) - Rate - Measurement - Networks - Reason geometrically |
(28 hours) - Rate - Measurement - Reason geometrically |
| Statistics and probability | (39 hours) - Quantify chance - Interpret chance - Collect and organise data - Represent data - Interpret data - Conduct chance experiments |
(36 hours) - Quantify chance - Interpret chance - Collect and organise data - Represent data - Interpret data |
(37 hours) - Quantify chance - Interpret chance - Represent data - Interpret data |
| Maths result | ATAR | GPA | ||
| Maths result | Pearson correlation (r value) | - | .806 | .502 |
| Significance (2-tailed) | - | <.001 | <.001 | |
| GPA | Pearson correlation (r value) | .502 | .533 | - |
| Significance (2-tailed) | <.001 | <.001 | - |
| Degree | Maths level (n) | Maths results | ATAR | GPA | |||
| Mean | SD | Mean | SD | Mean | SD | ||
| Overall | Elementary (18) Intermediate (79) Advanced (31) |
55.6 60.7 71.9 |
7.5 7.6 7.6 |
68.6 80.8 91.7 |
8.5 8.7 6.0 |
1.7 2.0 2.6 |
0.5 0.6 0.8 |
| 1. Biomedical Science |
Intermediate (5) Advanced (13) |
64.3**(a) 74.1 |
7.8 5.5 |
85.6**(a) 92.7 |
9.4 4.6 |
2.2**(a); *(b) 2.9 |
0.5 0.5 |
| 2. Exercise and Sports Science |
Elementary (5) Intermediate (19) Advanced (2) |
59.0 59.8 67.7 |
2.7 4.8 1.4 |
71.0 79.4 81.5 |
4.3 5.7 5.5 |
1.3 1.8 2.8 |
0.3 0.7 0.3 |
| 3. Physical Education |
Elementary (5) Intermediate (6) Advanced (1) |
57.6 53.4 55.4 |
8.5 6.7 0.0 |
70.2 72.5 84.0 |
9.0 2.4 0.0 |
1.8 1.8 1.8 |
0.3 0.2 0.0 |
| 4. Nursing | Elementary (8) Intermediate (35) Advanced (3) |
52.3 59.3 68.9 |
7.5 7.2 9.6 |
66.0 78.1 87.7 |
9.4 8.3 7.9 |
1.9 2.1 2.6 |
0.63*(c) 0.6 0.6 |
| 5. Physiotherapy | Intermediate (14) Advanced (12) |
67.4**(a) 72.3 |
6.7 7.6 |
91.5**(a) 93.9 |
2.8 4.3 |
2.0 2.3 |
0.5 1.0 |
| n = number of students enrolled; SD = standard deviation; * = significantly higher than other degrees (p <.05); ** = (p <.01); (a) Maths result for Biomedical Science is significantly higher than Exercise and Sports Science, Physical Education, and Nursing; (b) Maths result for Biomedical Science is significantly higher than Physiotherapy. (c) Maths result for Nursing is significantly higher than Physical Education. | |||||||
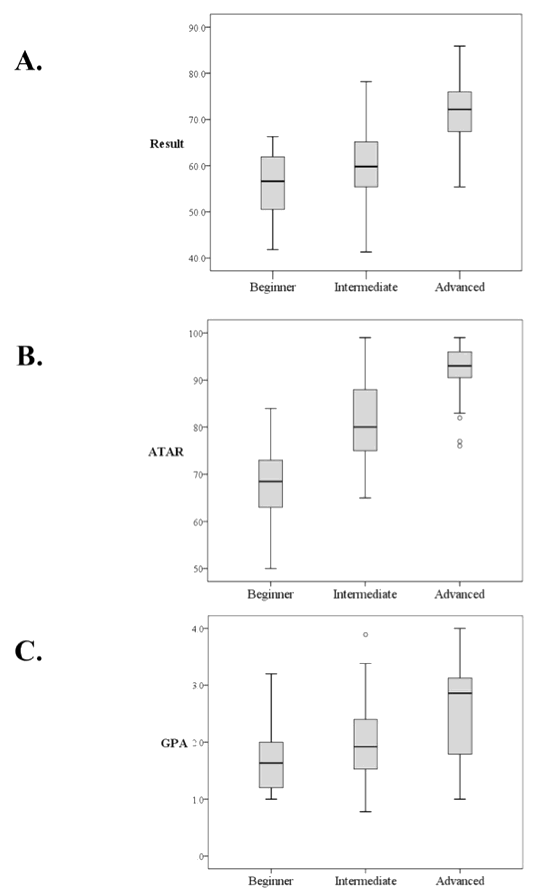
Figure 1: Boxplots summarising level of mathematics studied in secondary school
and
(A) mathematics result, (B) ATAR, and (C) GPA at the completion of first year
Finally, the second one-way ANOVA revealed significant between-degree main effects for both independent variables, 'result of completed level of mathematics at secondary school' (p < .01) and 'ATAR' (p < .01) with GPA as the dependent variable. Tukey post-hoc analyses of simple effects revealed Biomedical Sciences had significantly (p < .05) higher secondary school mathematics result over all other degrees, except for Physiotherapy. Physical Education was shown to have the lowest result of completed level of mathematics at secondary school score. For ATAR, Physiotherapy had significantly (p < .01) higher scores than all other degrees, apart from Biomedical Sciences (p > .05).
The results from the present study determined that the mathematics level studied by students entering university (directly from secondary school) significantly impacted on their performance in first year. Specifically, students who had previously studied advanced mathematics had a significantly higher first-year GPA over students studying either intermediate or elementary mathematics. Unsurprisingly, student competency in mathematics, and the mathematics level studied in secondary school, has previously been reported as a correlate of university success (Hine et al., 2015; Hourigan & Donoghue, 2007; Mills et al., 2009; Rylands & Coady, 2009). Another finding of this study agrees with these comments. When correlating level of mathematics studied and the corresponding result of that level of mathematics undertaken, those students who completed a lower level of mathematics did not attain a higher result, and those who completed a higher level of mathematics did attain a higher result [r(128) = .56, p < .01]. This is shown in Figure 1A. While linking achievement in mathematics and science has anecdotally been observed for some time, entering the first year of university with a high level of mathematics may allow students to comprehend subject matter in more applied university courses such as those in science disciplines (Nakakoji & Wilson, 2014). Biomedical Sciences and Physiotherapy had the highest percentage of students completing advanced mathematics at secondary school (72% and 46%, respectively). Exercise and Sports Science, Physical Education, and Nursing were all between 7% and 8%. The mathematics level previously studied is also a strong predictor for performance in first year anatomy and chemistry units (Anderton et al., 2016), which are particularly important for Biomedical Science and Physiotherapy students.
With regards to ATAR, students studying Physiotherapy entered university with significantly (p < .01) higher scores than all other degrees, apart from Biomedical Sciences (p > .05). Further, students from both these degrees displayed significantly higher GPAs at the completion of first year. As mentioned previously, a higher percentage of students entering into Biomedical Science and Physiotherapy degrees had previously studied more difficult mathematics, suggesting a possible cause for academic variability between degrees. While each of these degrees vary in theoretical and practical content, Biomedical Science students typically favour aspects of study relating to medical courses, such as anatomical dissections (Anderton et al., 2016). A high proportion of students undertaking Biomedical Sciences are using this degree as alternate entrance into Medicine. This would support the higher mathematics level previously studied for students undertaking the Biomedical Science degree. In comparison, students in other health science degrees may be more inclined to study broader aspects of the human body, involving human participants and peer-based activities (Anderton et al., 2016).
The results from the present study provide evidence linking the performance in mathematics level and academic success in degree studies, associated with a more focused structure and higher ATARs. One possible explanation for this is that participation in intermediate and advanced mathematics courses can encourage higher-order thinking skills, allow students to critically analyse situations, and extend their capacity to use mathematical concepts abstractly in real-life situations (Belward et al., 2011; McNaught & Hoyne, 2011). These required skills correspond to the associated careers of Biomedical Science and Physiotherapy students. As previously mentioned, the majority of students undertaking Biomedical Science are using this degree as an alternate pathway into medicine. Potential career earnings for the five degrees in this study report Biomedical Sciences and Physiotherapy average salaries at $100K+ and $70K+, respectively. These are reported to be greater than Physical Education ($60K+), Sports Science ($55K+), and Nursing (31K+) (Salary Comparison, 2017). It is therefore clear that undertaking a higher level of mathematics at secondary school not only relates to university performance, but also beyond.
Finally, students studying Biomedical Sciences and Physiotherapy attained a significantly (p <. 01) higher result in completed level of mathematics at secondary school, than students in the other three degrees. It is also important to note that both Biomedical Sciences and Physiotherapy degrees reported a greater percentage of students completing advanced mathematics than the other three degrees. The higher secondary school mathematics results scores of these students show they are more capable at understanding mathematics principles at a higher level, than students from the other three degrees, who recorded lower secondary school mathematics result scores from a lower level of mathematics studied (elementary or intermediate) (Hine et al., 2015; Hourigan & Donoghue, 2007; Mills et al., 2009; Rylands & Coady, 2009). As previously mentioned, those students who completed a lower level of mathematics did not attain a higher result, and those who completed a higher level of mathematics did attain a higher result. The similar findings for mathematics result with that of GPA and ATAR show a widening gap in academic achievement, dependent on the level of mathematics studied at secondary school that students enter university with. It could be suggested that modification of teaching and university courses to 'narrow' this gap could be considered, although factors such as known career path, study load, socio-economical bracket, and reasons for undertaking a tertiary education are outside the scope of this study.
The findings of this study should be considered along with some limitations. Firstly, this study was limited to school leavers only, who enter university immediately after finishing secondary school. However, in doing this, the authors were able to standardise the mathematics entry pre-requisites that may have differed from international and mature age students. Secondly, a positive and significant correlation existed between level of mathematics studied and the corresponding result [r(128) = .56, p < .01], indicating that those who undertook a higher level of mathematics obtained a higher result than those who undertook a lower level of mathematics and scored a lower result. However, despite this result it cannot be implied that a result in the lower level course is equivalent to the same result in a higher level course. Thirdly, although ATAR entry score for each degree differs, the level of difficulty between-degree cannot be objectively measured. Finally, and while this study examined the relationships between GPA, ATAR and level of mathematics completed, the authors acknowledge that a lower GPA or ATAR may not be solely attributable to mathematical background or ability.
It is hoped that the findings of this study will be useful to those personnel principally responsible for advising prospective entrants wishing to undertake study in a health science degree. For instance, the findings regarding mathematics and ATAR can inform the University's marketing approaches to senior secondary students, particularly those who intend commencing a health science degree. Furthermore, these findings can be used by staff working in secondary schools to counsel appropriately those students in lower secondary school (particularly Year 10 students) who are already considering subject selections for senior secondary school and for university entrance. Looking to the future, the researchers intend tracking the cohort of this study through to degree completion, in an attempt to investigate longitudinally the relationship between GPA, ATAR and secondary mathematics completed. Additionally, a further research topic has been identified for the researchers to explore the associations between GPA and scores in other subjects (i.e. other than mathematics) used to calculate a student's ATAR. Such investigations could provide additional insight into a between-degree comparison involving secondary mathematics and GPA.
Anderton, R. S., Hine, G. & Joyce, C. (2017). Secondary school mathematics and science matters: Predicting academic success for secondary students transitioning into university allied health and science courses. International Journal of Innovation in Science and Mathematics Education, 25(1), 34-47. https://openjournals.library.sydney.edu.au/index.php/CAL/article/view/11317/11058
Bacon, D. R. & Bean, B. (2006). GPA in research studies: An invaluable but neglected opportunity. Journal of Marketing Education, 28(1), 35-42. https://doi.org/10.1177/0273475305284638
Belward, S. R., Matthews, K. E., Thompson, K. V., Pelaez, N. J., Coady, C., Adams, P., Simbag, V. A. & Rylands, L. J. (2011). Applying mathematical thinking: The role of mathematicians and scientists in equipping the new generation scientist. In J. Hannah & M. Thomas (Eds.), Proceedings of Volcanic Delta 2011: The Eighth Southern Hemisphere Conference on Teaching and Learning Undergraduate Mathematics and Statistics, Rotorua, New Zealand, (12-21), 27 November - 2 December, pp.12-21.
Galligan, L., Loch, B. & Lawrence, J. (2010). Building academic numeracy in a first-year nursing course using an evaluative model of program development. Learning, Media and Technology, 33(3), 169-189. https://intranet.ecu.edu.au/__data/assets/pdf_file/0006/503853/Building-academic-numeracy-in-the-first-year-nursing-course-using-an-evaluative-model-of-program-development.pdf
Everett, J. E. & Robins, J. (1991). Tertiary entrance predictors of first year university performance. Australian Journal of Education, 35(1), 24-40. https://doi.org/10.1177/000494419103500105
Hall, J. M. & Ponton, M. K. (2005). Mathematics self-efficacy of college freshman. Journal of Developmental Education, 28(3), 26-32. https://eric.ed.gov/?id=EJ718579
Hine, G. S. C. (2015). Self-perceptions of pre-service mathematics teachers completing a Graduate Diploma of Secondary Education. Issues in Educational Research, 25(4), 480-500. http://www.iier.org.au/iier25/hine.html
Hine, G., Anderton, R. & Joyce, C. (2015). Mathematics: A good predictor for success in a health science degree. Proceedings of the Australian Conference of Science and Mathematics Education (pp. 114-117). Perth: Curtin University. http://openjournals.library.usyd.edu.au/index.php/IISME/article/view/8831
Hine, G., Reaburn, R., White, B., Carmichael, C., Galligan, L., Cavanagh, M., Anderson, J. & Ngu, B. (2016). Teaching secondary mathematics. Melbourne: Cambridge University Press.
Harackiewicz, J. M., Barron, K. E., Tauer, J. M. & Elliot, A. J. (2002). Predicting success in college: A longitudinal study of achievement goals and ability measures as predictors of interest and performance from freshman year through graduation. Journal of Educational Psychology, 94(3), 562-575. https://doi.org/10.1037/0022-0663.94.3.562
Hourigan, M. & O'Donoghue, J. (2007). Mathematical under-preparedness: The influence of the pre-tertiary mathematics experience on students' ability to make a successful transition to tertiary level mathematics courses in Ireland. International Journal of Mathematical Education in Science and Technology, 38(4), 461-476. http://dx.doi.org/10.1080/00207390601129279
Kajander, A., & Lovric, M. (2005). Transition from secondary to tertiary mathematics: McMaster University experience. International Journal of Mathematical Education in Science and Technology, 36(2-3), 149-160. http://dx.doi.org/10.1080/00207340412317040
Kennedy, J. P., Lyons, T. & Quinn, F. (2014). The continuing decline of science and mathematics enrolments in Australian high schools. Teaching Science, 60(2), 34-46. https://eprints.qut.edu.au/73153/
Koenig, K., Schen, M., Edwards, M. & Bao, L. (2012). Addressing STEM retention through a scientific thought and methods course. Journal of College Science Teaching, 41(4), 23-29. http://common.nsta.org/resource/?id=10.2505/4/jcst12_041_04_23
McPhan, G., Morony, W., Pegg, J., Cooksey, R. & Lynch, T. (2008). Maths? Why Not? Unpacking reasons for students' decisions concerning higher-level mathematics in the senior years. Report submitted to the Department of Education, Employment and Workplace Relations, March, pp.141. https://simerr.une.edu.au/pages/projects/10mathswhynot.php
McKenzie, K. & Schweitzer, R. D. (2001). Who succeeds at university? Factors predicting academic performance in first year Australian university students. Higher Education Research & Development, 20(1), 21-33. http://dx.doi.org/10.1080/07924360120043621
McNaught, K. & Hoyne, G. (2011). Mathematics for first year success. In Proceedings of the 14th Pacific Rim First Year in Higher Education Conference, 29 June - 1 July, Fremantle. http://fyhe.com.au/past_papers/papers11/FYHE-2011/content/pdf/4F.pdf
Messinis, G. & Sheehan, P. (2015). The academic performance of first year students at Victoria University by entry score and SES, 2009-2013. Analysis & Policy Observatory. http://apo.org.au/node/54684
Mills, C., Heyworth, J., Rosenwax, L., Carr, S. & Rosenberg, M. (2009). Factors associated with the academic success of first year Health Science students. Advances in Health Science Education, 14(2), 205-217. https://doi.org/10.1007/s10459-008-9103-9 [also https://espace.curtin.edu.au/handle/20.500.11937/33944]
Murphy, M., Papanicolaou, K. & McDowell, R. (2001). Entrance score and performance: A three year study of success. Journal of Institutional Research, 10(2), 32-49. http://www.aair.org.au/app/webroot/media/pdf/AAIR%20Fora/Forum1998/Murphy.pdf
Nakakoji, Y. & Wilson, R. (2014). Maths is a strong predictor of STEM attainment in first-year university. In Proceedings of the Australian Conference on Science and Mathematics Education, University of Sydney, pp. 149-155. https://openjournals.library.sydney.edu.au/index.php/IISME/article/view/7741
Nicholas, J., Poladian, L., Mack, J. & Wilson, R. (2015). Mathematics preparation for university: Entry, pathways and performance in first-year science and mathematics subjects. International Journal of Innovation in Science and Mathematics Education, 23(1), 37-51. https://openjournals.library.sydney.edu.au/index.php/CAL/article/view/8488
Sadler, P. M. & Tai, R. H. (2007). The two high-school pillars supporting college science. Science, 317(5837), 457-458. https://doi.org/10.1126/science.1144214
School Curriculum and Standards Authority (SCSA) (2007). Mathematics. Perth: SCSA. https://k10outline.scsa.wa.edu.au/home/p-10-curriculum/curriculum-browser/mathematics-v8
Rylands, L. J. & Coady, C. (2009). Performance of students with weak mathematics in first-year mathematics and science. International Journal of Mathematical Education in Science and Technology, 40(6), 741-753. http://dx.doi.org/10.1080/00207390902914130
Salary Comparison. (n.d.). Retrieved 1 May 2017 from http://www.payscale.com/
Tertiary Institutions Service Centre (TISC) (2016). TISCOnline. https://www.tisc.edu.au/static/guide/atar-about.tisc?cid=913932
Wright, K. (2007). Student nurses need more than maths to improve their drug calculating skills. Nurse Education Today, 27(4), 278-285. https://doi.org/10.1016/j.nedt.2006.05.007
Wright, V. J. (2015). Is ATAR useful for predicting the success of Australian students in initial teacher education? Australian Journal of Teacher Education, 40(9), 1-15. http://ro.ecu.edu.au/ajte/vol40/iss9/1/